Kezdőlap


Feladat:	924. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Várady Gábor
Füzet:	1959/május, 129 - 131. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Függvényvizsgálat, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1958/október: 924. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás: Kézenfekvőbb az olyan beírás (1. ábra), hogy a $K L M N$ négyzet $P Q$ oldalfelezője az $O A B$ körcikk szimmetriatengelyébe esik, de $φ \leq 90^{\circ}$ esetén olyan is lehetséges, hogy a körcikk ívére egy, a határoló sugaraira pedig két, ill. egy csúcsa esik a négyzetnek (2. ábra).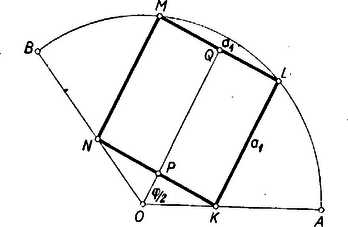¹

1. ábra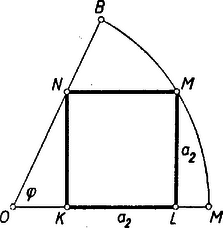

2. ábra

Eszerint miután majd e két lehetőség mellett felírtuk

φ

függvényeként a négyzet

a_{1}

, ill.

a_{2}

oldalából

t_{1} (φ)

, ill.

t_{2} (φ)

területét, a

0^{\circ} < φ \leq 90^{\circ}

szögekre meg kell vizsgálnunk, hogy

t_{1}

és

t_{2}

-nek melyike nagyobb. A nagyobb értéket adó kifejezés lesz a keresett függvény.
Az 1. ábra

O Q M

derékszögű háromszögéből a Pythagoras-tétel alapján, majd

O P

-t az

O P N

derékszögű háromszögből

φ / 2

-vel kifejezve

\begin{matrix} O M^{2} = 1 = O Q^{2} + Q M^{2} = {(O P + P Q)}^{2} + \frac{a_{1}^{2}}{4} = {(N P ctg \frac{φ}{2} + a_{1})}^{2} + \frac{a_{1}^{2}}{4} = \\ = {(\frac{a_{1}}{2} ctg \frac{φ}{2} + a_{1})}^{2} + \frac{a_{1}^{2}}{4} = \frac{a_{1}^{2}}{4} [{(ctg \frac{φ}{2} + 2)}^{2} + 1], \end{matrix}

és így

\begin{matrix} t_{1} = t_{1} (φ) = a_{1}^{2} = \frac{4}{{(ctg \frac{φ}{2} + 2)}^{2} + 1}, ha0^{\circ}<φ\leq180^{\circ}. \end{matrix}

(1)

Hasonlóan a 2. ábra

O L M

derékszögű háromszögéből

\begin{matrix} O M^{2} = 1 = O L^{2} + L M^{2} = {(O K + a_{2})}^{2} + a_{2}^{2} = {(N K ctg φ + a_{2})}^{2} + a_{2}^{2} = \\ = {(a_{2} ctg φ + a_{2})}^{2} + a_{2}^{2} = a_{2}^{2} [{(ctg φ + 1)}^{2} + 1], \end{matrix}

és így

\begin{matrix} t_{2} = t_{2} (φ) = a_{2}^{2} = \frac{1}{{(ctg φ + 1)}^{2} + 1}, ha0^{\circ}<φ\leq90^{\circ}. \end{matrix}

Elvben egyszerűbb volna a nagyobb területet

t_{1}

és

t_{2}

különbsége előjelét megvizsgálva kiválasztani. Mivel azonban

t_{1}

és

t_{2}

pozitív, és csak nevezőik változók, így a másodikat

4

-gyel bővítve az lesz a nagyobb, amelyikben a (módosítás utáni) nevező kisebb. Vizsgáljuk tehát ezek

\begin{matrix} k (φ) = {(ctg \frac{φ}{2} + 2)}^{2} + 1 - 4 {(ctg φ + 1)}^{2} - 4 \end{matrix}

különbségének előjelét a két függvény értelmezési tartományának közös részében, vagyis ha

0^{\circ} < φ \leq 90^{\circ}

Fejezzük ki

ctg φ

-t is

ctg \frac{φ}{2} = x

-szel:

\begin{matrix} ctg φ = \frac{cos φ}{sin φ} = \frac{{cos}^{2} \frac{φ}{2} - {sin}^{2} \frac{φ}{2}}{2 sin \frac{φ}{2} cos \frac{φ}{2}} = \frac{{ctg}^{2} \frac{φ}{2} - 1}{2 ctg \frac{φ}{2}} = \frac{x^{2} - 1}{2 x}, \end{matrix}

így a különbség

x

függvényeként:

\begin{matrix} k (φ) = k_{1} (x) = {(x + 2)}^{2} - 4 {(\frac{x^{2} - 1}{2 x} + 1)}^{2} - 3 = \frac{1}{x^{2}} (- x^{2} + 4 x - 1) = \frac{f x}{x^{2}} . \end{matrix}

Meg kell állapítanunk

k_{1} (x)

-nek az új változó szerinti értelmezési tartományát.

0^{\circ} < \frac{φ}{2} \leq 45^{\circ}

folytán

ctg \frac{φ}{2} = x \geq 1

; ezekre az

x

-ekre vizsgáljuk

k_{1} (x)

-et. Előjele csak az

f (x) = {- x}^{2} + 4 x - 1 = 3 - {(x - 2)}^{2}

másodfokú függvény előjelétől függ. Ez pozitív a

2 - \sqrt[]{3}

és

2 + \sqrt[]{3}

közti

x

-ekre, minden más

x

-re negatív, vagy

0

, azonban az előbbi érték nem tartozik bele

k_{1} (x)

értelmezési tartományába. Így

k_{1} (x) = k (φ)

egyszer megváltoztatja előjelét.
Eszerint

t_{1}

és

t_{2}

nagyságviszonya nem állandó, hanem egyszer ellentétesre fordul, éspedig

x = ctg \frac{φ}{2} = 2 + \sqrt[]{3}

-nál; ekkor

ctg φ = \sqrt[]{3}

, és így

φ = 30^{\circ}

, és

φ / 2 = 15^{\circ}

. Valóban,

k_{1} (2 + \sqrt[]{3}) = k (30^{\circ}) = 0

, és

t_{1} (30^{\circ}) = t_{2} (30^{\circ}) = (5 - 2 \sqrt[]{3}) / 13

.
A nagyságviszonyról előrebocsátottak értelmében

1 \leq x = ctg \frac{φ}{2} < 2 + \sqrt[]{3}

esetén, vagyis mivel a kotangens függvény csökkenő,

45^{\circ} \geq φ / 2 > 15^{\circ}

, másképpen

90^{\circ} \geq φ > 30^{\circ}

esetén

k_{1} (x) = k (φ)

pozitív, tehát

t_{1}

kisebb

t_{2}

-nél, a körcikk ilyen nyílásszöge esetén a nemszimmetrikusan beírt négyzet területe nagyobb. ‐ Viszont

x = ctg \frac{φ}{2} > 2 + \sqrt[]{3}

, azaz

φ / 2 < 15^{\circ}

φ < 30^{\circ}

esetén az előjel és a nagyságviszony ellentétes, a szimmetrikusan beírt négyzet a nagyobb területű.

φ > 90^{\circ}

mellett csak az első beírási mód használható, akkor

t_{1}

adja a keresett függvényt. ‐ Mindezek szerint a keresett

t (φ)

függvényt két képlettel így írhatjuk fel:

\begin{matrix} t (φ) = {\begin{matrix} \frac{4}{{(ctg \frac{φ}{2} + 2)}^{2} + 1}, ha0^{\circ}<φ\leq30^{\circ}és ha90^{\circ}<φ\leq180^{\circ},\frac{1}{{(ctg φ + 1)}^{2} + 1}, ha30^{\circ}\leqφ\leq90^{\circ}. \end{matrix} \end{matrix}

φ = 30^{\circ}

-ra mindkét képlet érvényes.

Várady Gábor (Győr, Révai M. g. III. o. t.)

Megjegyzés. Figyeljük meg, hogy

90^{\circ}

-nál

t (90^{\circ}) = t_{2} (90^{\circ})

nagyobb, mint

t_{1} (90^{\circ})

, és nagyobb szögekre

t (φ)

ehhez a kisebb értékhez csatlakozik. Első pillantásra meglepő, hogy eszerint pl.

90^{\circ}

-os körcikkből nagyobb négyzetlemezt lehet kivágni, mint

100^{\circ}

-osból; ne felejtsük el azonban azt a követelményt, hogy a négyzetlemez csúcsainak a körcikklemez kerületén kell lenniük.

¹Meg lehet mutatni, hogy más megfelelő beírási lehetőség nincs.