Kezdőlap


Feladat:	911. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágh A. , Arató P. , Bartha L. , Biborka Tamás , Bollobás B. , Bondy T. , Elbert Á. , Endrődy T. , Füle K. , Gaál S. , Győry K. , Halász G. , Katona Gy. , Kolonits F. , Koszterszitz Gy. , Leipniker P. , Losonczy L. , Makay A. , Megyesi L. , Mihályffy L. , Montvay I. , Náray Miklós (Bp.) , Papp Éva , Pásztor Erzsébet , Pődör B. , S. Nagy Erzsébet , Sárközy A. , Simon L. , Simon László , Simonfai L. , Soós S. , Szász D. (III. o.) , Szatmári G. , Szekér A. , Tatai P. , Tóth Zsuzsanna , Trón T.
Füzet:	1959/március, 80 - 83. oldal		PDF \| MathML
Témakör(ök):	Súlypont, Egyenesek egyenlete, Pont és egyenes távolsága, Egyenes, Feladat
Hivatkozás(ok):	Feladatok: 1958/május: 911. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Előkészítésül megmutatjuk, hogy az $A B C$ háromszög $S$ súlypontján átmenő egyeneseknek a háromszögtől mért középtávolsága 0. Ha egy ilyen $e$ éppen súlyvonal, pl. $A A'$ ‐ ahol $A'$ a $B C$ oldal felezőpontja ‐, akkor $A$ távolsága $e$ -től 0, az $e$ -nek két partjára eső $B$ és $C$ -nek $B B_{1}$ , ill. $C C_{1}$ távolságai pedig az $A' B B_{1}$ és $A' C C_{1}$ derékszögű háromszögek egybevágósága folytán (átfogó és két szög) egyenlők, és így a középtávolságot adó különbség valóban $0$ . Minden más esetben az $S$ -en áthaladó $e_{0}$ egyenes egy csúcsot elválaszt a másik kettőtől, legyen ez $A$ . A másik parton fekvő $B$ és $C$ távolságainak, mint a $B B_{0} C_{0} C$ trapéz (a $0$ index az $e_{0}$ -on levő vetületet jelöli) párhuzamos oldalainak összege egyenlő a középvonalnak, $A'$ $e_{0}$ -tól mért $A' A'_{0}$ távolságának kétszeresével; ugyanennyi $A$ -nak $e_{0}$ -tól való $A A_{0}$ távolsága is, mert az $S A' A'_{0}$ és $S A A_{0}$ háromszögek hasonlók (két szög), és így a súlypont harmadoló tulajdonságánál fogva $A A_{0} : A' A'_{0} = S A : S A' = 2 : 1$ , vagyis $A A_{0} = 2 A' A'_{0}$ . Ezek szerint a képezendő különbség ismét 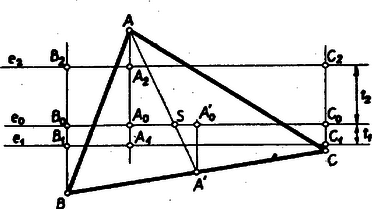$0$ .

Most megmutatjuk, hogy ha az

e

egyenes párhuzamos

e_{0}

-val és távolságuk

t

, akkor

e

-nek a háromszögtől mért középtávolsága

3 t

e

e_{0}

-ból a mindkettőjükre merőleges egyenes mentén

t

-vel való eltolással is előállítható. Eközben

e

-nek az egyes csúcsoktól mért távolsága vagy növekszik ‐ ti. ha

e

e_{0}

-nak a csúccsal ellentétes partján van ‐, vagy csökken, ha a csúccsal megegyező partján, és 0-ra csökken, ha

e

átmegy a csúcson. (Egyelőre olyan legyen

e

, amely ugyanúgy választja szét

A

B

C

-t mint

e_{0}

, azaz eltolással nem lép át csúcsot.) Pl. az ábrán

e_{1}

azon a partján van

e_{0}

-nak, mint

B

és

C

, így

e_{1}

A

-tól messzebb,

B

és

C

-hez közelebb van, mint

e_{0}

e_{2}

viszont

A

-hoz közelebb,

B

és

C

-től távolabb van mint

e_{0}

; így középtávolságuk:

\begin{matrix} A A_{1} - (B B_{1} + C C_{1}) = 3 t_{1}, ill . (B B_{2} + C C_{2}) - A A_{2} = 3 t_{2}, \end{matrix}

mert egy tag nőtt és két tag csökkent

t_{l}

-gyel, ill. két tag nőtt és egy tag csökkent

t_{2}

-vel (az

e_{0}

-ra fentebb kapott 0 középértékhez képest).
A középtávolság megállapításában az abszolút értéket a példákban úgy kaptuk meg, hogy a különbségben a megnövekedett távolságot (ill. távolságok összegét) vettük kisebbítendőnek. Ezt úgy is mondhatjuk, hogy a három csúcs távolságát előjelesen összeadtuk, és ebben azon csúcsoknak

e

-től mért távolságát vettük negatívnak, amelyek

e_{0}

-nak ugyanazon partján vannak, mint

e

, az ellentett parton levőket pedig pozitívnak. Továbbfejlesztve: azt, hogy a negatívnak vett távolságok abszolút értéke

t

-vel csökkent, és a pozitívnak vetteké

t

-vel növekedett, úgy mondhatjuk, hogy minden (előjeles) távolságot

t

-vel növeltünk, így növekedett a háromtagú összeg

3 t

-vel. Ezek a megállapításaink már olyan

e

-kre is érvényesek, amelyekbe az

e_{0}

eltolásával egy, vagy két csúcs átlépése után jutunk el, és így a középtávolságnak az eredeti előírás szerinti képezésében a levonandók hozzáadandóvá válnak, megfelelően annak, hogy

t

hozzáadásával az eredetileg negatív távolság pozitívvá lett.
Ha már most a súlyponttól

t

távolságra eltolt egyenes középtávolsága

3 t

, akkor a

d

középtávolságú egyenesek azok és csak azok, amelyek a súlyponttól

d / 3

távolságra vannak, azaz amelyek érintik a súlypont körül

d / 3

sugárral írt kört.

Simon László (Bp. XI., József A. g. IV. o. t.)

II. megoldás: Legyenek az adott háromszög csúcsai valamely derékszögű koordinátarendszerben

P_{1} (x_{1}, y_{1})

P_{2} (x_{2}, y_{2})

P_{3} (x_{3}, y_{3})

, és legyen az

y = m x + b

egyenesnek e háromszögtől mért középtávolsága

d

. Ekkor felhasználva a pontnak egyenestől mért távolságára a koordinátageometriából ismert képletet:

\begin{matrix} d = d_{1} + d_{2} + d_{3} = | \frac{y_{1} - m x_{1} - b}{\sqrt[]{m^{2} + 1}} + \frac{y_{2} - m x_{2} - b}{\sqrt[]{m^{2} + 1}} + \frac{y_{3} - m x_{3} - b}{\sqrt[]{m^{2} + 1}} | . \end{matrix}

Itt nem volt szükség

d

-nek

d_{1}

d_{2}

d_{3}

-ból összeadással, összeadás és kivonással való képezésére, esetek széjjelválasztására, ugyanis a képlet már előjellel adja a távolságot aszerint, hogy a pont az egyenesnek egyik vagy másik partján van.
Átrendezéssel

\begin{matrix} | \frac{\frac{y_{1} + y_{2} + y_{3}}{3} - m \frac{x_{1} + x_{2} + x_{3}}{3} - b}{\sqrt[]{m^{2} + 1}} | = \frac{d}{3}, \end{matrix}

továbbá, felismerve a bal oldali számlálóban háromszögünk

S

súlypontjának

y_{s}

x_{s}

koordinátáit:

\begin{matrix} | \frac{y_{s} - m x_{s} - b}{\sqrt[]{m^{2} + 1}} | = \frac{d}{3}, \end{matrix}

ez pedig azt jelenti, hogy az

y = m x + b

egyenes

S

-től

d / 3

távolságban van, érinti az

S

körül

d / 3

sugárral írt kört. Az átalakításokat visszafelé olvasva belátható, hogy minden az

S

körül

d / 3

sugárral írt kört érintő egyenesnek a háromszögtől való középtávolsága

d

Biborka Tamás (Makó, József A. g. I. o. t.)