Kezdőlap


Feladat:	909. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Andréka B. , Arató P. , Bartha L. , Biborka T. , Bollobás B. , Bondy T. , Elbert Á. , Endrődy T. , Füle K. , Gaál S. , Galambos János , Gergely Cs. , Győry K. , Hadik Z. , Hainzmann J. , Halász G. , Hank Zs. , Katona Gy. , Kisvölcsey J. , Kolonits F. , Koszterszitz Gy. , Kristóf L. , Losonczy L. , Makay A. , Megyesi L. , Meskó A. , Mihályffy L. , Molnár Márta , Montvay I. , Muszély Gy. , Pásztor Erzsébet , Pődör Bálint , Rátkay Zs. , S. Nagy Erzsébet , Sárközy András , Sátori Gy. , Simon L. , Simonfai L. , Soós S. , Szász D. (III. o.) , Tatai P. , Tóth Zsuzsanna , Trón L. , Trón T. , Tusnády Gábor , Újváry-Menyhárt Zoltán , Várallyay L.
Füzet:	1959/február, 54 - 58. oldal		PDF \| MathML
Témakör(ök):	Hiperbola egyenlete, Síkgeometriai szerkesztések, Hiperbola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1958/május: 909. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyenek az adott elemek rendre $O$ , $x$ , $P_{1}$ , és $P_{2}$ , továbbá az $O$ -ban $x$ -re merőlegesen álló képzetes tengely $y$ , végül a keresett aszimptoták $u$ és $v$ .
Feltehetjük, hogy $P_{1}$ és $P_{2}$ az $x$ és $y$ által létrehozott síknegyedek közül ugyanegyben van pl. $x$ és $y$ -t a koordinátatengelyek szokásos irányításába állítva a jobb felső I. negyedben, esetleg egyikük az $x$ -en, vagyis a hiperbola egyik ágának ugyanazon a felén; ugyanis a II., III., vagy IV. negyedben adott pontok esetén $y$ -ra, $O$ -ra, ill. $x$ -re való tükrözéssel a mondott helyzet előállítható. Feltesszük továbbá, hogy $P_{1}$ és $P_{2}$ az esetleges ilyen tükrözések után is különböző pontjai a hiperbolának, ‐ azaz $O P_{1} \neq {O P}_{2}$ és az indexek alkalmas megválasztásával $O P_{1} < O P_{2}$ ‐, természetesen $O$ -tól is különböznek, és a $P_{1} P_{2}$ egyenes $x$ , $y$ egyikével sem párhuzamos, és nem megy át $O$ -n. A kizárt esetekben ugyanis vagy nincs meghatározva a hiperbola, vagy nem létezik a követelményeket kielégítő hiperbola.
$O$ ismeretében elegendő az aszimptotáknak egy-egy $O$ -tól különböző pontját megszerkeszteni; keressük azt az $U$ , ill. $V$ pontjukat, ahol a $P_{1} P_{2}$ egyenest metszik (1. ábra).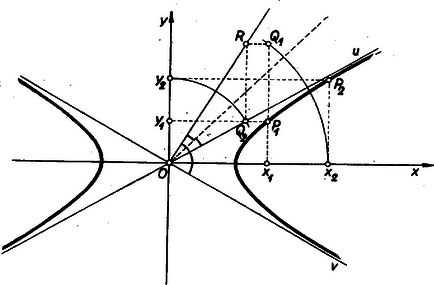

1. ábra

Ezek a

P_{1}

P_{2}

pontpárra tett feltevés folytán egyrészt léteznek ‐ ugyanis

P_{1} P_{2}

nem lehet

u

és

v

egyikével sem párhuzamos, mert aszimptotával párhuzamos egyenesen a hiperbolának nem lehet két pontja, ‐ másrészt

O

-tól és így egymástól is különbözők,

O

-val együtt háromszöget alkotnak,

U

és

V

egyike az I., másika a IV. negyedben van.
Ismeretes, hogy a hiperbola bármely húrjának felezőpontja egyben a húrt kimetsző egyenesnek az aszimptoták közti szakaszát is felezi; eszerint

P_{1} P_{2}

-nek

p

felezőmerőlegese egyben az

O U V

háromszög

U V

oldalát is merőlegesen felezi. Tudjuk továbbá, hogy

u

és

v

tükrös egyenespár a tengelyekre nézve, eszerint

x

és

y

adják az

O U V

háromszög

O

csúcsánál levő belső és külső szögek felezőit, mégpedig

x

,,pozitív'' oldala a belső szögfelező, mint az

U

V

-t tartalmazó I. és IV. síknegyed elválasztó vonala. Minthogy pedig a háromszög bármelyik csúcsából kiinduló belső és külső szögfelezőpár a szemközti oldal felező merőlegeséből a körülírt kör egy átmérőjét metszi ki, azért

p

-nek

x

, ill.

y

-nal való

Q_{1}

Q_{2}

metszéspontjai között megkapjuk a háromszög körülírt körének egy átmérőjét, és e körnek

P_{1} P_{2}

-vel való metszéspontjaiban a keresett

U

V

-t.
Az elemzésből a szerkesztés lépései:

O

-n át meghúzzuk az

x

-re merőleges

y

-t,

P_{1} P_{2}

felező merőlegesének az

x

és

y

közé eső

Q_{1} Q_{2}

szakasza mint átmérő fölé

k

kört írunk, ebből

P_{1} P_{2}

-vel kimetsszük

U

V

-t, végül

O U

és

O V

megrajzolásával megkapjuk az

u

v

aszimptotákat. ‐ Változat:

y

és

Q_{2}

mellőzhetők:

k

-nak

K

középpontját

P_{1} P_{2}

és

O Q_{1}

felező merőlegeseinek metszéspontja is megadja, sugara pedig

r = K O = K Q_{1}

.
Valóban, a kapott

U

V

pontokra

U P_{1} = V P_{2}

és

x

felezi a

V O U

szöget, ezért

O U

és

O V

aszimptoták.
Mindezekből azt is látjuk, hogy ha a feladat megoldható, akkor csak egy megoldás (egy

u

v

pár) van. A megoldhatóság feltétele, hogy

p

messe

x

és

y

mindegyikét, azaz

P_{1} P_{2}

x

-szel, se

y

-nal ne legyen párhuzamos. Ezt a

P_{1}

P_{2}

párra tett feltevésünk már biztosítja, ugyanis

p

csak úgy lehetne párhuzamos a tengelyek valamelyikével, ha ugyanez

P_{1} P_{2}

-re is állna. Végül, hogy

x

-nek pozitív oldala belső szögfelezője legyen az

O U V

háromszögnek, hogy a két szimmetriatengely közül ez legyen a valós tengely, ehhez szükséges, hogy az

O P_{1} P_{2}

háromszög a csúcsok ezen sorrendjében pozitív körüljárású legyen, másszóval az oldalai közti

O P_{1} < O P_{2}

egyenlőtlenséggel együtt az ezen oldalai és

x

pozitív fele közti

α_{1}

és

α_{2}

szögekre ugyanezen értelemben

α_{1} < α_{2}

álljon.

Galambos János (Veszprém, Lovassy L. G. IV. o. t.)

Megjegyzés.

P_{1}

és

P_{2}

-nek az I. negyedbe való rögzítésével tulajdonképpen csak az elemzést és a diszkussziót könnyítettük meg. A szerkesztés bármely

P_{1}

P_{2}

pontpárral végrehajtható, hacsak

p

metszi

x

és

y

mindegyikét. Az ellentétes eset pedig azt jelenti, hogy

P_{1}

és

P_{2}

vagy tükrösek,

x

és

y

és

O

egyikére, vagyis az adatok nem függetlenek egymástól, vagy pedig a feladat megoldhatatlan, az adatok ellentmondásban vannak (pl. ha

x

merőleges

P_{1} P_{2}

-re, de nem felező merőlegese a

P_{1} P_{2}

szakasznak). Ha

α_{1}

α_{2}

-vel az

O P_{1}

O P_{2}

egyeneseknek

x

-szel bezárt hegyes szögét jelölve

O P_{1} < O P_{2}

és

α_{1} > α_{2}

, akkor

x

nem valós, hanem képzetes tengelye lesz a hiperbolának.

II. megoldás: Legyen

P_{1} P_{2}

metszéspontja

x

y

-nal

S_{1}

, ill.

S_{2}

, és

P_{1} P_{2}

felezőpontja

T

. Ekkor a szögfelezők által létrehozott szakaszokra vonatkozó tétel szerint az

O U V

háromszögben

\begin{matrix} S_{1} U : S_{1} V = O U : O V = S_{2} U : S_{2} V . \end{matrix}

Itt az első és a harmadik arány tagjait olyan szakaszok összegével, ill. különbségével helyettesíthetjük, amelyeknek egyik végpontja

T

\begin{matrix} (T U + T S_{1}) : (T V - T S_{1}) = (T S_{2} + T U) : (T S_{2} - T V) . \end{matrix}

Innen egyrészt

T V = T U

figyelembevételével, másrészt mindkét arány helyett a tagjai összegéből és különbségéből képezett arányra áttérve

\begin{matrix} 2 T U : 2 T S_{1} = 2 T S_{2} : 2 T U, \end{matrix}

amiből

\begin{matrix} T U^{2} = T S_{1} \cdot {T S}_{2}, \end{matrix}

vagyis

U

és

V

-nek a megszerkeszthető

T

-től az ismert

P_{1} P_{2}

egyenesen mért távolsága mértani középarányos a megszerkeszthető

T S_{1}

és

T S_{2}

szakaszok között.

Tusnády Gábor (Sátoraljaújhely, Kossuth L. g. III. o. t.)

III. megoldás: Legyen az adott

O

és

x

origója, ill.

X

tengelye egy derékszögű koordinátarendszernek és legyenek az adott pontok koordinátái ebben a rendszerben

P_{1} (x_{1}

y_{1})

, ill.

P_{2} (x_{2}

y_{2})

. Ekkor hiperbolánk egyenlete

\begin{matrix} \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 \end{matrix}

alakú. Itt az ismeretlen

a

és

b

meghatározhatók volnának abból a két egyenletből álló

\begin{matrix} \frac{x_{1}^{2}}{a^{2}} - \frac{y_{1}^{2}}{b^{2}} = 1, & (1) \\ \frac{x_{2}^{2}}{a^{2}} - \frac{y_{2}^{2}}{b^{2}} = 1 & (2) \end{matrix}

egyenletrendszerből, amely azt fejezi ki, hogy

P_{1}

és

P_{2}

rajta vannak a hiperbolán, most azonban az aszimptoták

\pm b / a

iránytangense céljára csak arányukra van szükség. (1) és (2) kivonásával és alkalmas rendezéssel

\begin{matrix} \frac{b}{a} = \frac{\sqrt[]{y_{2}^{2} - y_{1}^{2}}}{\sqrt[]{x_{2}^{2} - x_{1}^{2}}} \end{matrix}

(3)

és ez, ill. az aszimptoták derékszögű háromszögek révén megszerkeszthetők pl. a következő lépésekben: az

O

körül

x_{2}

, ill.

y_{2}

sugárral rajzolt, I. negyedbeli negyedköríveket metsszük, éspedig az előbbit a

P_{1}

-en át az

X

-tengelyre, az utóbbit az

Y

-tengelyre állított merőlegessel, majd a kapott

Q_{1}

-en át az

Y

-ra,

Q_{2}

-n át az

X

-re állított merőlegesnek

R

metszéspontját összekötjük

O

-val. Ekkor

O R

-nek

α

irányszögére

tg α = a / b

, ennélfogva

u

-t

O R

-nek az I. negyed szögfelezőjére való tükrözésével,

v

-t pedig

O

-ban az

O R

-re állított merőlegesként kaphatjuk (2. ábra).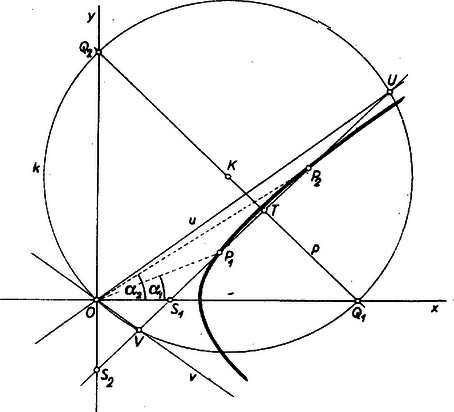

2. ábra

(3)-ban feltettük, hogy

x_{2} > x_{1} (> 0)

, így a nevezőbeli gyök alatt pozitív szám áll. Ehhez (1) és (2)-t, valamint az

y_{1} \geq 0

y_{2} > 0

feltevéseket hozzávéve már következik, hogy

y_{2} > y_{1}

, vagyis (3) számlálója is valós, ugyanis

\begin{matrix} \frac{y_{2}^{2}}{b^{2}} = \frac{x_{2}^{2}}{a^{2}} - 1 > \frac{x_{1}^{2}}{a^{2}} - 1 = \frac{y_{1}^{2}}{b^{2}} . \end{matrix}

Sárközy András (Gyöngyös, Vak Bottyán g. IV. o. t.)

IV. megoldás: Az adott két pont, valamint

x

y

és

O

-ra vonatkozó tükörképeik közül választott 5 pont felhasználásával a kúpszeletbe írt hatszögre vonatkozó Pascal-tétel alapján megszerkeszthetjük e pontok bármelyikében a hiperbola érintőjét.^{$^{*}$} Láttuk továbbá a 847. feladat II. megoldásában,^{$^{*}$} hogy egy

P

hiperbolapont és a benne húzható

e

érintő, valamint az

x

y

tengelyek ismeretében hogyan szerkeszthetők meg az

F_{1}

F_{2}

fókuszok: annak a körnek az

x

valós tengely egyenesévél való metszéspontjaiként, amelynek középpontja az

y

képzetes tengelyen van, és amely átmegy

P

-n, valamint

e

és

y

-nak

C

metszéspontján. Végül a 847. feladat III. megoldásában^{$^{*}$} látott tétel megfordításával

F_{1}

F_{2}

P

és

e

ismeretében megszerkeszthetjük

e

-nek az aszimptotákkal való metszéspontjait: az az

F_{1}

F_{2}

-n átmenő kör metszi ki ezeket, amelynek középpontját a

P

-ben

e

-re emelt merőleges metszi ki

y

-ból.

Pődör Bálint (Bp. II., Rákóczi F. g. IV. o. t.)

Megjegyzés. A fókuszok ismeretében a szerkesztést annak alapján is folytathatjuk, hogy

F_{1}

F_{2}

-nek

e

-n való

F'_{1}

F'_{2}

merőleges vetületei rajta vannak az

O

közepű,

a

sugarú főkörön; így az

O F_{1} = c

átfogóból és az

O F'_{1} = a

befogóból szerkesztett derékszögű háromszög másik befogójában megkapjuk

b

-t, végül

b / a

-ban az aszimptoták iránytangensét.

^{$^{*}$}Lásd pl. Schopp János: Kúpszeletek (Középisk. Szakköri Füzet), Tankönyvkiadó, 1955. 73‐74. o., 68. és 70. §.

^{$^{*}$}KML. XVI. kötet 89. o. (1958 március).

^{$^{*}$}K. M. L. XVI. kötet 89. o. (1958 március).