Kezdőlap


Feladat:	902. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Rátkay Zsolt , Sárközy András
Füzet:	1959/január, 22 - 23. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1958/április: 902. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyenek egy a $C$ közepü, $r$ sugarú körnek $A C B ∢ = 2 α$ nyílásszöge $C A B$ körcikkébe az előírt módon beírt $D E F G$ téglalapnak az $\hat{A B}$ íven fekvő csúcsai $D$ és $E$ , a $C B$ ill. $C A$ sugáron fekvők pedig $F$ , ill. $G$ . A $D E$ szakasz $f$ felező merőlegese egyrészt a téglalap egyik szimmetriatengelye és így $F G$ -nek is felező merőlegese, másrészt ‐ mint egy húr felező merőlegese ‐ átmegy $C$ -n. Ezek szerint $C F = C G$ , tehát a $C F G$ háromszög egyenlő szárú és $f$ az $A C B$ szöget is felezi. Így a $D$ csúcs megválasztása után az $A C B$ szög felezőjével húzott párhuzamos ill. rá merőleges egyenesek révén a beírt téglalap meg van határozva.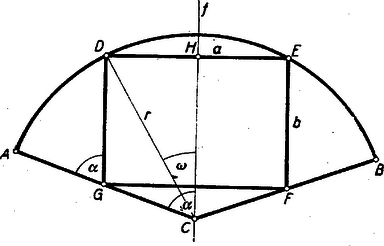

A keresett téglalapnak valamely szerkeszthető jellemző adatát kell megállapítanunk, válasszuk erre a célra a

C D

sugárnak

f

-fel bezárt

ω

szögét.
Téglalapunk területe

4

-szer akkora, mint a

C D G

háromszög területe, mert ez utóbbinak a

D G = b

alaphoz tartozó magassága egyenlő

D H = a / 2

-vel; elegendő tehát

D

-t úgy meghatározni, hogy e háromszög területe legyen maximális. Ebben a

C D = r

oldal, valamint ennek

G

-ben mért

C G D ∢ = 180^{\circ} - α

látószöge állandók, ezért rögzített

C D

esetén

G

mértani helye a

C D

-hez mint húrhoz tartozó,

180^{\circ} - α

szögű látószögkörív, és így a

C D G

háromszög területe akkor maximális, ha

G

az ív ,,legmagasabb'' pontjában van, azaz, ha a háromszög egyenlő szárú. Ekkor

G C D ∢ = (180^{\circ} - C G D ∢) / 2

, azaz

α - ω = α / 2

ω = α / 2

, vagyis a maximális területet adó

D

pont az

\hat{A B}

ív negyedében van, az

A C H

szög felezőjével metszhető ki.

Sárközy András (Gyöngyös, Vak Bottyán g. IV. o. t.)

II. megoldás: A szerkesztés előkészítéséül a beírható legnagyobb területű téglalapot úgy is meghatározhatjuk, hogy a területet

ω

függvényeként írjuk fel és ennek állapítjuk meg a maximumát. A téglalap két oldala a

C D E

egyenlő szárú háromszögből, ill. a szinusz tétellel a

C D G

háromszögből:

\begin{matrix} a = 2 r sin ω, ill. b \frac{r sin (α - ω)}{sin (180^{\circ} - α)} = \frac{r sin (α - ω)}{sin α}, \end{matrix}

így a területe ‐ a két változó szög szinuszának szorzatát az ismert

2 sin x sin y = cos (x - y) - cos (x + y)

azonosság alapján különbséggé alakítva:

\begin{matrix} t = a b = \frac{r^{2}}{sin α} \cdot 2 sin ω sin (α - ω) = \frac{r^{2}}{sin α} [cos (2 ω - α) - cos α] . \end{matrix}

t

akkor a legnagyobb, amikor ezen kifejezés egyetlen változó része a legnagyobb:

cos (2 ω - α) = 1

2 ω - α = 0^{\circ}

ω = α / 2

Rátkay Zsolt (Bp. VI., Kölcsey F. g. III. o. t.)

Megjegyzés. Ábránk ‐ a szokásnak megfelelően ‐ félkörnél kisebb körcikket, szektort mutat. Ámde két nem egymás meghosszabbításába eső sugár a kört két körcikkre vágja szét, ezek egyike konkáv. (Kör alakú

%

-os grafikonokon a szocialista szektort rendszerint ilyen ábrázolja.) Eredményünk konkáv körcikkre nem a körcikklemezből kivágható legnagyobb területű téglalapot adja meg, hanem a legnagyobb olyat, amelynek 2‐2 csúcsa a körcikk ívén, ill. a sugarakon vagy az azokat hordozó,

C

-végpontú félegyeneseken van (aszerint, hogy

2 α \leq 240^{\circ}

, vagy

2 α > 240^{\circ}