Kezdőlap


Feladat:	899. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Nagy Judit
Füzet:	1959/január, 17 - 19. oldal		PDF \| MathML
Témakör(ök):	Harmadfokú (és arra visszavezethető) egyenletek, Paraméteres egyenletek, Gyökök és együtthatók közötti összefüggések, Feladat
Hivatkozás(ok):	Feladatok: 1958/április: 899. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Tegyük fel, hogy a pozitív $u$ szám gyöke egyenletünknek, azaz fennáll az

\begin{matrix} u^{3} - a u^{2} - b u - c = 0 \end{matrix}

(1)

egyenlőség. Megmutatjuk, hogy nincs az egyenletnek

u

-nál nagyobb gyöke, azaz nincs olyan pozitív

y

, amellyel

u + y

is gyök.
Egyenletünk bal oldala

x = u + y

helyettesítéssel, majd (1) figyelembevételével így alakítható:

\begin{matrix} y^{3} + (3 u - a) y^{2} + (3 u^{2} - 2 a u - b) y + (u^{3} - a u^{2} - b u - c) = \\ = y [y^{2} + (3 u - a) y + (3 u^{2} - 2 a u - b)] = y (y^{2} + p y + q) . \end{matrix}

Itt feltevéseink folytán mindkét együttható pozitív, ugyanis (1) felhasználásával

\begin{matrix} p = 3 u - a = 2 u + (u - a) = 2 u + \frac{b u + c}{u^{2}} > 0, \\ q = 3 u^{2} - 2 a u - b = u^{2} + u (u - a) + (u^{2} - a u - b) = \\ = u^{2} + \frac{b u + c}{u} + \frac{c}{u} > 0, \end{matrix}

ennélfogva az

y (y^{2} + p y + q)

kifejezés értéke minden

y > 0

-ra pozitív, valóban seholsem 0.
Megállapításunkat a legkisebb pozitív gyökre alkalmazva adódik, hogy az az egyetlen pozitív gyök.
Hasonló átalakítással bármely olyan polinomra belátható az ún. ,,Descartes‐féle jelszabály'' érvényessége, amelyben egyetlen ,,jelváltás'' lép fel.

II. megoldás: Jelöljük az adott egyenlet gyökeit

x_{1}

x_{2}

x_{3}

-mal és fejtsük ki polinommá az egyenletnek a gyöktényezős alakját. Mivel

x^{3}

együtthatója 1:

\begin{matrix} (x - x_{1}) (x - x_{2}) (x - x_{3}) = x^{3} - (x_{1} + x_{2} + x_{3}) x^{2} + \\ + (x_{1} x_{2} + x_{1} x_{3} + x_{2} x_{3}) x - x_{1} x_{2} x_{3} = 0, \end{matrix}

azért a gyökök és az első együttható megegyezése folytán ennek és az adott egyenletnek minden további együtthatója megegyezik:

\begin{matrix} x_{1} + x_{2} + x_{3} = a, & (1) \\ x_{1} x_{2} + x_{1} x_{3} + x_{2} x_{3} = - b, & (2) \\ x_{1} x_{2} x_{3} = c . & (3) \end{matrix}

Tegyük fel egyelőre, hogy mind a három gyök valós, és egyik sem 0. Ekkor (3)-ból

c \neq 0

, így a három gyök szorzata feltevésünk folytán:

c > 0

, ez pedig csak úgy lehetséges, ha a negatív gyökök száma páros: 2 vagy 0, és így a pozitívok száma 1 vagy 3. Három pozitív gyök lehetőségét azonban (2) kizárja, mert aszerint a kéttényezős szorzatok

- b

összege nem pozitív, itt tehát a pozitív gyökök száma valóban pontosan 1.
Ha a gyökök közül pontosan egy, pl.

x_{3} = 0

, úgy összefüggéseink egyszerűsödnek:

\begin{matrix} x_{1} + x_{2} = a, & (1a) \\ x_{1} x_{2} = - b (> 0), & (2a) \end{matrix}

és (

2 a

)-ból nyilvánvaló, hogy ‐ az állításnak megfelelően ‐ egy pozitív és egy negatív gyök van.
Ha

x_{2} = x_{3} = 0

, akkor már nincs mit bizonyítanunk.
Ha pedig egyenletünknek komplex gyöke is van, pl.

x_{1} = p + q i

, ahol

p

és

q

valósak és

q \neq 0

, azaz fennáll:

\begin{matrix} (p^{3} - a p^{2} - b p - c - 3 p q^{2} + a q^{2}) + (3 p^{3} - 2 a p - b - q^{2}) q i = 0, \end{matrix}

ami azt jelenti, hogy mindkét zárójeles kifejezés 0 (azt természetesen feltételezzük, hogy

a

b

c

valósak), akkor

x_{1}

-nek

x_{2} = p - q i

konjugáltja ‐ amelyre

x_{2} \neq x_{1}

‐ ugyancsak gyök, így a három gyök közül ismét legfeljebb egy lehet pozitív.

Nagy Judit (Szombathely, Kanizsai Dorottya lg. III. o. t.)

Megjegyzés: Néhány ,,második megoldás'' az egyenletet

x^{3} = a x^{2} + b x + c

alakba írva a pozitív gyökök számáról a ,,jól ismert''

y = x^{3}

és

y = a x^{2} + b x + c

görbék grafikonja alapján a következőképpen kívánt tájékozódni.
,,A valós gyököket a két görbe közös pontjaihoz tartozó abszcisszák adják. Az

y = x^{3}

görbe mindenütt emelkedve a III. negyedből az origón át az I. negyedbe lép, menetéből minket csak az I. negyedbeli ív érdekel. Pozitív

x

-ekre az

y = a x^{2} + b x + c

görbe is mindenütt emelkedik (pontosabban: sehol sem süllyed); ugyanis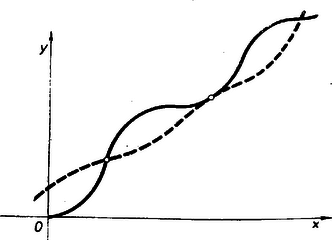

a \neq 0

esetén az

\begin{matrix} y = a {(x + \frac{b}{2 a})}^{2} + \frac{4 a c - b^{2}}{4 a} \end{matrix}

átalakítás szerint a parabola csúcsa ,,alul'' van éspedig a nem pozitív

x_{0} = - \frac{b}{2 a}

abszcisszán;

a = 0

, és

b \neq 0

esetén

b > 0

és így az

y = b x + c

egyenes minden

x

-re emelkedik; végül

a = b = 0

esetén az

y = c (\geq 0)

egyenes párhuzamos az

X

-tengellyel. Minthogy továbbá az

y = a x^{2} + b x + c

görbe az I. negyedbe az

Y

-tengely

c \geq 0

ordinátájú pontján át lép be, azért a két görbének az I. negyedben csak egy közös pontja lehet''.

Ebben a meggondolásban csak az utolsó mondat hibás; nem biztos ugyanis, hogy két emelkedő görbeív legfeljebb egy pontban metszi egymást, emelkedés közben ,,kanyarogva'' ábránk szerint akárhány közös pontjuk lehet. Az ilyen megoldások szerzői burkoltan a vizsgált görbék ,,simaságára'', keveset kanyargó voltára gondoltak. Az I. megoldás tulajdonképpen azt mutatta meg, hogy az

u

abszcisszájú közös ponttól jobbra nem lehet további közös pont, mert minden

x > u

-ra az

y = x^{3}

görbe ordinátája nagyobb az

y = a x^{2} + b x + c

görbe ordinátájánál.
Tanulságul jegyezzük meg: a szemlélet gyakran jó ötleteket ad, de rendszerint egyes esetre vonatkozik és így forrása lehet elsietett általánosításoknak.