Feladat: 895. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Ágh A. ,  Arató P. ,  Bárczy P. ,  Beke G. ,  Bender Cecilia ,  Bollobás B. ,  Bondy T. ,  Bornes Klára ,  Dániel G. ,  Elbert Á. ,  Endrődy T. ,  Fanta Katalin ,  Füle K. ,  Galambos J. ,  Grallert F. ,  Győry K. ,  Halász G. ,  Kisvölcsey J. ,  Kolonits Ferenc ,  Kristóf L. ,  Leipniker P. ,  Makay A. ,  Máté L. ,  Mayer G. ,  Megyesi L. ,  Meskó A. ,  Mester Z. ,  Montvay I. ,  Mózes E. ,  Nagy Elemér ,  Náray Miklós (Bp.) ,  Papp Éva ,  Pásztor Erzsébet ,  Pataki Zsuzsanna ,  Pödör B. ,  S. Nagy Erzsébet ,  Sárközy A. ,  Simon L. ,  Simonfai L. ,  Soós S. ,  Szász D. ,  Szatmári G. ,  Szekér A. ,  Tatai P. ,  Tóth Zsuzsanna ,  Tusnády Gábor ,  Tusnády László ,  Várallyay L. 
Füzet: 1958/december, 153 - 154. oldal  PDF  |  MathML 
Témakör(ök): Tetraéder magasságpontja, Tetraéderek, Feladat
Hivatkozás(ok):Feladatok: 1958/március: 895. matematika feladat

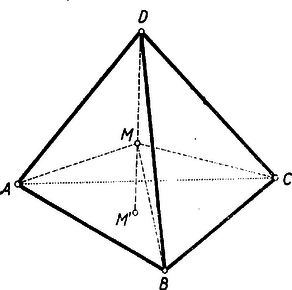
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Elég megmutatnunk, hogy az ABCM tetraédernek mind a négy magasságvonala átmegy D-n, vagyis D ortocentruma, magasságpontja ABCM-nek. Az M-ből kiinduló magasság, azonos MD-vel, mert ABCD ortocentrikussága folytán D-nek és M-nek közös az ABC-n való merőleges vetülete, éspedig az ABC▵ magasságpontja. * Az A-ból kiinduló magasság AD, mert egyrészt ABCD ortocentrikus és így BC⊥AD, másrészt BM-nek az ACD lapra való merőlegességéből BM⊥AD, eszerint a BC és BM egyenesekkel meghatározott BCM sík és AD merőlegesek egymásra. B és C ugyanolyan kapcsolatban vannak M és D-vel, mint A, ezért a B-ből és C-ből induló magasságvonalak is átmennek D-n, és ezzel bizonyításunkat befejeztük.

 

Kolonits Ferenc (Bp. VIII., Piarista g. III. o. t.)
 

Megjegyzések. 1. Az A-ból kiinduló magasságra vonatkozó meggondolás elveszti alapját, ha a BC és BM egyenesek egybeesnek, más szóval, ha M ráesik BC-re. Ez a körülmény az 1 alatt idézett tulajdonsággal egybevetve azt jelenti, hogy ilyenkor az ABC▵ M' magasságpontja BC-n van, ami ‐ mint könnyen belátható ‐ csak úgy lehetséges, ha e háromszög B vagy C-nél derékszögű. Ilyenkor M' és vele M ezen derékszög csúcsába esik, így az ABCM, ABDM, ACDM és BCDM tetraéderek közül három síkidommá fajul el, a negyedik azonos ABCD-vel és állításunk értelmetlenné, ill. ismétléssé válik.
2. Könnyű belátni, hogy a D csúcs ABC-n való merőleges vetületének az ABC▵ M' magasságpontjával való egybeesése elegendő feltétel ahhoz, hogy az ABCD tetraéder ortocentrikus legyen. Eszerint M helyett a DM' magasságvonalnak M' kivételével bármely pontja az A, B, C csúcsokkal együtt ortocentrikus tetraédert határoz meg.
 

 

3. Az ABCM ortocentirikussága így is belátható: AM a magasságpont értelmezésénél fogva merőleges a BCD síkra, és így a benne fekvő BC egyenesre; hasonlóan BM és AC, valamint CM és AB is merőlegesek. Így azonban még hátra van annak megmutatása, hogy az ortocentrum éppen az M-mel felváltott D csúcsban van.
*Lásd KML. XVI. köt. 34. o.