Kezdőlap


Feladat:	894. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kisvölcsey Jenő , Szebeni András
Füzet:	1958/december, 152 - 153. oldal		PDF \| MathML
Témakör(ök):	Tetraéder magasságpontja, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1958/március: 894. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Tekintsük az $A B C D$ ortocentrikus tetraéder $A B$ és $C D$ éleit. Minthogy ezek merőlegesek egymásra, azért mindegyiken át fektethető egy és csak egy a másikra merőleges sík; jelöljük ezeknek a $C D$ , ill. az $A B$ egyenessel való metszéspontját $T_{1}$ , ill. $T_{2}$ -vel. A $T_{1} T_{2}$ egyenes mindkét síkban benne van, ez a metszésvonaluk.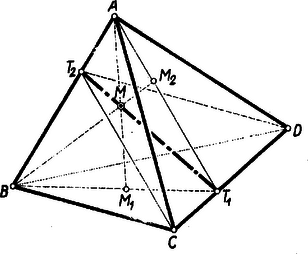

A B T_{1}

síknak minden egyenese, így

T_{1} T_{2}

, továbbá

A T_{1}

és

B T_{1}

merőleges

C D

-re, hasonlóan

C D T_{2}

-nek

T_{1} T_{2}

, valamint

C T_{2}

és

D T_{2}

egyenesei merőlegesek

A B

-re. Eszerint egyrészt

T_{1} T_{2}

A B

és

C D

egyenesek mindegyikére merőleges, mindegyikét metszi, tehát ez az (egyetlen) normál tranzverzálisuk, másrészt

T_{1}

, ill.

T_{2}

A C D

és

B C D

, ill.

C A B

és

D A B

lapháromszögek

A T_{1}

és

B T_{1}

, ill.

C T_{2}

és

D T_{2}

lap-magasságainak a

C D

, ill.

A B

oldalon való talppontjai. Ezzel a feladat második állítását a vizsgált élpárra vonatkozóan bebizonyítottuk.
Minthogy egyetlen élnek sincs a többivel szemben valami megkülönböztető tulajdonsága, azért bizonyításunk bármelyik szemközti élpárra érvényes. Ugyanígy a feladat első állításának bizonyításában is elég lesz egy élpárral és normál tranzverzálisával foglalkozni.
A tetraéder

A

-ból vont

A M_{1}

magassága merőleges a

B C D

lap síkjára, ennek minden egyenesére, így

C D

-re is, ennélfogva benne van az egyetlen olyan síkban, amely átmegy

A

-n és merőleges

C D

-re, vagyis

A B T_{1}

-ben. Ugyanígy a

B

-ből vont

B M_{2}

magasság is benne van

A B T_{1}

-ben, következésképpen ez áll a tetraéder

M

magasságpontjára is mint

A M_{1}

és

B M_{2}

metszéspontjára. Hasonlóan a

C

és

D

csúcsokból vont magasságvonalakkal együtt a

C D T_{2}

síkban is benne van

M

, ennélfogva e két síknak

T_{1} T_{2}

metszésvonalán is. Ezzel a feladat első állítását is bebizonyítottuk.

Szebeni András (Bp. I., Petőfi S. g. IV. o. t.)

Megjegyzés. Bizonyításunkból az is következik, hogy a normál tranzverzálisoknak a lapsíkokra való merőleges vetületei a lapok magasságvonalaira esnek.

II. megoldás: A normál tranzverzálisoknak

M

-en való áthaladását abból is beláthatjuk, hogy

A M_{1}

merőleges a

B C D

síknak

B T_{1}

egyenesére, ugyanígy

B M_{2}

merőleges az

A C D

sík

A T_{1}

egyenesére, ezért

A M_{1}

és

B M_{2}

egyszersmind az

A B T_{1} ▵

-nek is egy-egy magasságvonala, ennélfogva

M

metszéspontjukon ‐ amely feltevésünk szerint a tetraéder mind négy magasságának közös pontja ‐ a háromszög harmadik magasságvonala is átmegy. Ez pedig éppen a

T_{1} T_{2}

normáltranzverzális, amelynek

A B

-re merőleges voltát már fentebb láttuk.

Kisvölcsey Jenő (Bp. VIII., Piarista g. III. o. t.)