Kezdőlap


Feladat:	886. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ágh A. , Andréka Bertalan , Arató P. , Bartha L. , Bender Cecilia , Bollobás B. , Endrődy T. , Füle K. , Galambos J. , Gereben Ildikó , Grallert F. , Gyene A. , Győry K. , Hadik Z. , Halász G. , Hank Zs. , Kisvölcsey J. , Kolonits F. , Kristóf László , Máté L. , Megyesi L. , Mester Z. , Mihályffy L. , Mózes E. , Pataki Zsuzsanna , Pődör B. , Sárközy A. , Simonfai L. , Szász D. , Szatmári G. , Várallyay L.
Füzet:	1958/november, 109 - 112. oldal		PDF \| MathML
Témakör(ök):	Poliéderek hasonlósága, Térfogat, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1958/február: 886. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Vegyük észre a hasonlóságot egyrészt a bizonyítandó, másrészt a 878. feladatban bebizonyított összefüggések között; ennek alapján átvehetjük az ott használt bizonyítási módszereket.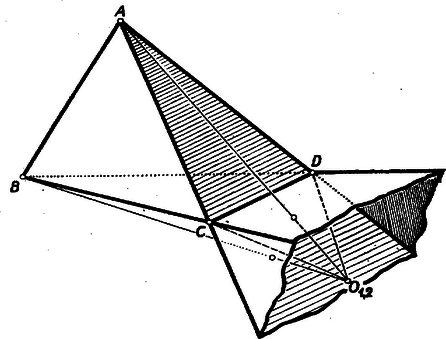
Láttuk a külső érintő gömbök vizsgálatánál,¹ hogy a tetraéder két szemközti éléhez, pl. az $A B$ -hez és a $C D$ -hez tartozó vályúszerű térrészek közül csak egyikben lehet külső érintő gömb. Tegyük fel, hogy a $C D$ élhez tartozó vályúban van külső érintő gömb. Kössük össze ennek $O_{12}$ középpontját $A$ , $B$ , $C$ , $D$ -vel. Így ahhoz a négy újabb tetraéderhez jutunk, melyeknek közös csúcsa $O_{12}$ és evvel szemközti lapjuk az eredeti tetraéder egy-egy lapja.

1. ábra

O_{12}

ből kiinduló magasságvonal hossza mindegyikben

ϱ_{12}

O_{12}

-ből a

C D

-ben összefutó

B C D

és

A C D

lapoknak a külső oldalát látjuk, ezért, ha itt is az

A

B

C

D

és a gömbközéppont által meghatározott konvex test köbtartalmát tekintjük, akkor ezt az eredeti, valamint a

B C D O_{12}

és az

A C D O_{12}

tetraéderek köbtartalmának összege adja. Másrészt

O_{12}

ből az egymást

A B

-ben metsző

A B D

és

A B C

lapoknak a belső oldalát látjuk (ti.

B C D

-t és

A C D

-t átlátszónak tekintve), ennélfogva az

A B D O_{12}

és

A B C O_{12}

tetraéderek együtt ugyanazt a teret töltik ki, mint az előbbi három tetraéder. Ebből; az eredeti tetraéder köbtartalmát

K

-val, az

A

B

C

D

csúccsal szemben fekvő lapjának területét

t_{1}

t_{2}

t_{3}

t_{4}

-gyel jelölve:

\begin{matrix} K + \frac{t_{1} ϱ_{12}}{3} + \frac{t_{2} ϱ_{12}}{3} = \frac{t_{3} ϱ_{12}}{3} + \frac{t_{4} ϱ_{12}}{3} . \end{matrix}

Innen

ϱ_{12}

reciprokát kifejezve:

\begin{matrix} \frac{1}{ϱ_{12}} = \frac{t_{3}}{3 K} + \frac{t_{4}}{3 K} - \frac{t_{1}}{3 K} - \frac{t_{2}}{3 K} . \end{matrix}

(1)

Itt a jobboldali hányadosokat kifejezhetjük a (felbontatlan)tetraéder köbtartalmának képlete alapján a megfelelő magasságvonalak hosszával:

\begin{matrix} K = \frac{t_{i} m_{i}}{3} -ból \frac{t_{i}}{3 K} = \frac{1}{m_{i}}, (i = 1, 2, 3, 4) . \end{matrix}

(2)

Ezeket (1)-be helyettesítve

\begin{matrix} \frac{1}{ϱ_{12}} = \frac{1}{m_{3}} + \frac{1}{m_{4}} - \frac{1}{m_{1}} - \frac{1}{m_{2}}, \end{matrix}

(3)

vagyis b)-nek azt az esetét kapjuk, amelyben a bal oldal előtt

+

jel áll.
A másik eset hasonlóan adódik abból a feltevésből, hogy az

A B

élhez tartozó vályúban van külső érintő gömb. Ekkor a felsorolt lap-párok ill. a rajtuk álló,

O_{12}

csúcsú tetraéder-párok szerepet cserélnek, (3) megfelelőjében mindegyik magasság ellentett jellel adódik, és b)-nek második esetét az egyenlőségnek

(- 1)

-gyel való szorzásával kapjuk meg.
a) igazolásához helyettesítsük a jobb oldalon a sugarak reciprok értékét a 878. feladatbeli c) és a megfelelő további összefüggések alapján a magasságok reciprok értékével (l. a megoldásban (3) alatt, ezen szám 98. o.). Így

\begin{matrix} \frac{1}{ϱ_{1}} + \frac{1}{ϱ_{2}} - \frac{1}{ϱ_{3}} - \frac{1}{ϱ_{4}} = \frac{- 1 + 1 - 1 - 1}{m_{1}} + \frac{1 - 1 - 1 - 1}{m_{2}} + \frac{1 + 1 + 1 - 1}{m_{3}} + \\ + \frac{1 + 1 - 1 + 1}{m_{4}} = 2 (\frac{1}{m_{3}} + \frac{1}{m_{4}} - \frac{1}{m_{1}} - \frac{1}{m_{2}}), \end{matrix}

ez pedig (3) szerint valóban egyenlő

\pm \frac{2}{ϱ_{12}}

-vel.

Andréka Bertalan (Győr, Czuczor G. g. III. o. t.)

II. megoldás: A b) összefüggés más igazolása a következő: Tegyük fel, hogy a

C D

élhez tartozó vályúban van külső érintőgömb, vagyis olyan, amely az

A B C

A B D

lapok síkját ugyanazon az oldalukon érinti, amelyen a tetraéder van, a

B C D

A C D

lapok síkját pedig a másik oldalról, mint amelyen a tetraéder van, és jelöljük e gömb középpontját

O_{12}

-vel. Fektessünk ehhez az

A C D

lappal párhuzamosan érintősíkot és jelöljük e síknak a

B A

B C

B D

félegyenesekkel való metszéspontjait sorra

A_{1}

C_{1}

D_{1}

-gyel (2. ábra).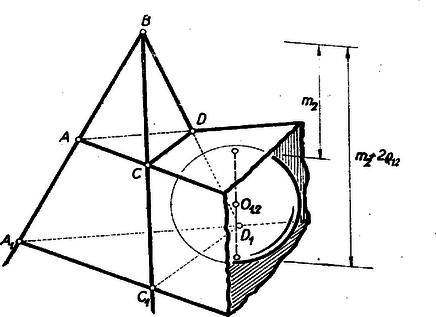

2. ábra

A létrejött

A_{1} B C_{1} D_{1}

tetraéder hasonló

A B C D

-hez,

B

-ból kiinduló magasságáínak hossza

m_{2} + 2 ϱ_{12}

. Gömbünk

A_{1} B C_{1} D_{1}

-nek is mind a négy lapsík ját érinti, de csak a

B C_{1} D_{1}

lapot érinti kívülről, tehát ebben a tetraéderben azt a szerepet játssza, amit

A B C D

-ben a

ϱ_{1}

sugarú gömb. E gömbök sugarának és a

B

csúcsból húzott magasságoknak aránya a hasonlóság folytán egyenlő:

\begin{matrix} \frac{ϱ_{12}}{ϱ_{1}} = \frac{m_{2} + 2 ϱ_{12}}{m_{2}} = 1 + \frac{2 ϱ_{12}}{m_{2}}, \end{matrix}

innen

ϱ_{12}

reciprokát kifejezve:

\begin{matrix} \frac{1}{ϱ_{12}} = \frac{1}{ϱ_{1}} - \frac{2}{m_{2}}, \end{matrix}

végül a 878. feladat c) összefüggése alapján ismét (3) adódik.

Kristóf László (Mosonmagyaróvár, Kossuth L. g. IV. o. t.)

Megjegyzések: Igazolhatjuk a b) összefüggést a 878. feladat megjegyzésében idézett tétel alkalmazásával is.
Bizonyításunkból az is kiolvasható, hogy akkor van külső érintő gömb a

C D

élhez tartozó vályúban, ha (3) jobb oldala pozitív, vagyis, ha

\begin{matrix} \frac{1}{m_{3}} + \frac{1}{m_{4}} > \frac{1}{m_{1}} + \frac{1}{m_{2}}, \end{matrix}

másképpen (2) felhasználásával, ha

\begin{matrix} t_{3} + t_{4} > t_{1} + t_{2} . \end{matrix}

Általában: a tetraéder valamely éléhez tartozó vályúszerű térrészben akkor és csak akkor van külső érintő gömb, ha az élben találkozó lapok területének összege kisebb a másik két lap területösszegénél. Ha e két összeg egyenlő, akkor a két szemközti él egyikének vályúszerű térrészében sincs érintő gömb; emiatt van csak öt érintő gömbje a szabályos tetraéder lapsíkjainak.

¹Molnár Ferenc: A tetraéder nevezetes pontjairól (1. közlemény), KML. XVI. kötet 4. o., 1958 január.