Kezdőlap


Feladat:	883. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Beke Géza , Ducza Lajos , Gaál Sándor , Máthé Csaba , Nagy Balázs , Tusnády László
Füzet:	1958/november, 105 - 106. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat, Beírt kör, Hossz, kerület, Számtani-mértani egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1958/február: 883. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Kérdésünk így is fogalmazható: a szóbanforgó háromszögek melyikében maximális a két befogó összege? Ezen összeg előállítása végett mérjük rá egy az állandó $A B$ átfogón álló tetszés szerinti $A B C$ derékszögű háromszög $A C$ befogójának $C$ -n túl való meghosszabbítására a $C B$ -vel egyenlő $C B'$ szakaszt és vizsgáljuk $A B' = A C + C B$ változását (1. ábra).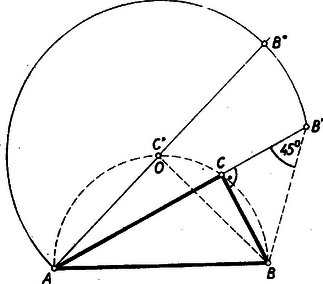

1. ábra

Az egyenlő szárú derékszögű

C B B'

háromszög révén

A B' B ∢ = 45^{\circ}

, eszerint

B'

rajta van

A B

-nek

45^{\circ}

nyílású látószögkörívén. E körív

O

középpontjából

A B

látószöge

2 \cdot 45^{\circ} = 90^{\circ}

, eszerint

O

A B

átmérőjű Thales-félkörnek az

A B

felező merőlegesével való metszéspontja.

A B'

a látószögkörív egy részének húrja, ennélfogva akkor maximális, ha

B'

A

-nak a körívbeli átellenes pontjába,

B^{*}

-ba esik, vagyis

A B^{*}

átmegy

O

-n. Ekkor a megfelelő

C^{*}

B

-ből

A B^{*}

-ra bocsátott merőleges talppontjába,

O

-ba esik, és így a keresett maximális kerületű háromszög az

A B O

egyenlő szárú derékszögű háromszög.

Beke Géza (Hatvan, Bajza J. g. III. o. t.)

Megjegyzés: Hasonlóan látható be, hogy az adott alappal és ezzel szemben tetszés szerinti adott szöggel bíró háromszögek közül is az egyenlő szárúnak van maximális kerülete.

II. megoldás: Ismert összefüggés szerint derékszögű háromszögben a szokásos jelölésekkel:

a + b = c + 2 ϱ

, ahol

ϱ

a beírt kör sugara. Így

a + b + c = 2 c + 2 ϱ

ugyanakkor maximális, mint ez a sugár.
Másrészt tudjuk (I. gimn. tankönyv), hogy a beírt kör

O

középpontja azon a köríven van, amelynek pontjaiból az

A B

szakasz látószöge

135^{\ci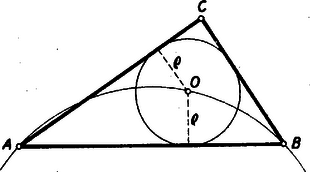rc}

(2. ábra).

2. ábra

Nyilván akkor legnagyobb

ϱ

, ha

O

ezen körív felezőpontjában,

A B

felezőmerőlegesén van; ekkor pedig szimmetria folytán a háromszög egyenlő szárú.

Gaál Sándor (Veszprém, Lovassy L. g. III. o. t.)

III. megoldás:

a + b + c

akkor maximális, amikor

a + b

; ez akkor, amikor

{(a + b)}^{2}

; ez ‐ az

\begin{matrix} {(a + b)}^{2} = a^{2} + b^{2} + 2 a b = c^{2} + 2 a b = c^{2} + 4 t = c^{2} + 2 c m_{c} \end{matrix}

átalakítás alapján ‐ akkor, amikor

a b

, ill.

t

c m_{c}

ill.

m_{c}

maximális. Már most

m_{c}

legnagyobb értéke a Thales félkörben

\frac{c}{2}

és evvel a háromszög egyenlő szárú, a kerülete

c (1 + \sqrt[]{2})

Máthé Csaba (Győr, Révay M. g. II. o. t.)

IV. megoldás: A III. megoldáshoz kapcsolódva

a b

-re a következő egyenlőtlenség áll:

\begin{matrix} a b = \sqrt[]{a^{2} b^{2}} ≦ \frac{a^{2} + b^{2}}{2} = \frac{c^{2}}{2}; \end{matrix}

a b

fel is veszi a legnagyobb értéket, és

a b = \frac{c^{2}}{2}

-ből

a = b

Nagy Balázs (Eger, Dobó I. g. IV. o. t.)

V. megoldás: Az

y = a + b + c = c (1 + sin α + cos α)

függvénynek ugyanott van maximuma, ahol a

z = sin α + cos α

-nak, ill. ‐ mivel itt

0^{\circ} < α < 90^{\circ}

folytán mindkét tag pozitív ‐ ahol

v = {(sin α + cos α)}^{2} = 1 + sin 2 α

-nak. Ez

2 α = 90^{\circ}

-nál következik be, akkor pedig

α = 45^{\circ} = β

Ducza Lajos (Székesfehérvár, József A. g. IV. o. t.)

VI. megoldás: Az előbbi

z

függvény maximumát így is megkaphatjuk:

\begin{matrix} sin α + cos α = sin α + sin (90^{\circ} - α) = 2 sin \frac{α + 90^{\circ} - α}{2} cos \frac{α - (90^{\circ} - α)}{2} = \sqrt[]{2} cos (α - 45^{\circ}) \end{matrix}

maximális, ha

cos (α - 45^{\circ}) = 1

α - 45^{\circ} = 0^{\circ}

α = 45^{\circ} = β

Tusnády László (Sátoraljaújhely, Kossuth L. g. IV. o. t.)