Feladat: 879. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bollobás Béla ,  Győry K. ,  Halász G. ,  Kolonits F. ,  Leipniker P. ,  Makay A. ,  Megyesi László ,  Pásztor Erzsébet ,  Pődör B. ,  Sárközy A. ,  Szász D. ,  Tatai P. ,  Tóth Zsuzsanna ,  Várallyay L. 
Füzet: 1958/november, 99 - 101. oldal  PDF  |  MathML 
Témakör(ök): Beírt kör, Tetraéderek, Feladat
Hivatkozás(ok):Feladatok: 1958/január: 879. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Láttuk a tetraéderről szóló cikkben,1 hogy a három szemközti élpár páronkénti összegeinek megegyezése szükséges feltétele (bebizonyítható következménye) az élérintő gömb létezésének. Most a feltétel elegendő voltát kell bizonyítanunk. Hogy bizonyításunkhoz kiindulópontot kapjunk, megemlítjük az élérintő gömb létezésének még egy következményét. Nyilvánvaló, hogy ha van a tetraédernek élérintő gömbje, akkor ezt mindegyik lapsík körben metszi, és a metszési kör azonos a megfelelő lapháromszög beírt körével; továbbá, hogy bármelyik két ilyen kör egymást is érinti. (Különböző síkokban fekvő körökre is akkor mondjuk, hogy érintik egymást, ha van közös pontjuk és abban közös az érintő egyenesük.)
Megmutatjuk, hogy a tetraédernek a feltevés szerinti

a+a'=b+b'=c+c'(1)
tulajdonságából (l. a jelöléseket az ábrán) ugyancsak következik, hogy bármelyik két lapháromszögéhez tartozó beírt körök érintik egymást.
 

 

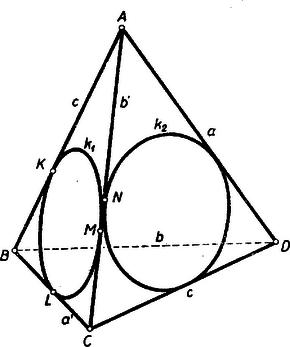Tekintsük pl. az ABC és ACD háromszögek k1, ill. k2 beírt körét és jelöljük az AC élen levő érintési pontjukat M, ill. N-nel, az ABC, ill. ACD háromszög félkerületét s1, ill. s2-vel. Ekkor ismert összefüggés szerint
AM=s1-a=b'+(c'-a')2,AN=s2-c=b'+(a-c)2,


és innen, mivel (1) folytán a két zárójelbeli különbség egyenlő, AM=AN adódik, azaz M és N egybeesnek, k1 és k2 valóban érintik egymást, és ez áll bármelyik két beírt körre is.
A négy tetraéderlaphoz tartozó négy beírt kör egy gömbön van. Ugyanis pl. a k1 beírt körön átmenő (e kört tartalmazó) gömbök középpontjának mértani helye a k1 középpontjában az ABC lapsíkra merőleges e1 egyenes (a kör ,,tengelye''). Bármelyik két ilyen tengely metszi egymást, mert egy síkban vannak ‐ pl. e1 és az ACD lapsíkra merőleges e2 az M≡N érintési ponton átmenő, az AC élre merőleges síkban, ‐ és nem párhuzamosak (ugyanis szögük méri az ABC és ACD lapsíkok szögét, ami sem nem 0∘, sem nem 180∘). Ennélfogva az e1, e2, e3, e4 tengelyek a 471. gyakorlatban bebizonyított tétel szerint egy O pontban metszik egymást (ugyanis nem lehetnek egy síkban, mert különben a rájuk merőleges négy lapsík merőlegesen állana a tengelyek közös síkjára, akkor pedig ugyanez állana a lapsíkok páronkénti metszésvonalaira, az élek egyeneseseire is, vagyis mind a hat él párhuzamos volna). Ez az O pont a négy beírt kör páronkénti, összesen hat érintkezési pontjától ugyanakkora távolságban van. Bármelyik lap beírt körének három érintési pontjára nyilván igaz ez ‐ pl. az ABC lapon K, L, M-re OK=OL=OM ‐, ezek viszont a további három lapból még egy-egyben játsszák ugyanezt a szerepet, és így az egyenlőség átjut O-nak a további három él-érintési ponttól való távolságára. Végül az OK, OL, ill. OM szakasz merőleges az AB, BC, ill. AD élre, mert pl. OM a fentiek szerint benne van e1 és e2 közös síkjában, és ez áll a további esetekben is, ‐ ennélfogva az O körül OK sugárral írt gömb valóban érinti a tetraéder valamennyi élét. Ezzel bizonyításunkat befejeztük.
 

Megyesi László (Makó, József A. g. IV. o. t.)
 

II. megoldás: Vegyünk át az I. megoldásból annyit, hogy pl. az A csúcsban találkozó három háromszöglap beírt körei páronként érintik egymást éspedig különböző pontban. Másrészt ez a három kör nincs egy síkban. Ezekből már következik,2 hogy egy gömbön vannak. Ez a gömb a három háromszög oldalaiként a tetraédernek mind a hat élét érinti.
 

Bollobás Béla (Bp. V., Apáczai Csere J. gyak. g. I. o. t.)

1Molnár Ferenc: A tetraéder nevezetes pontjairól (I. közlemény), K. M. L. XVI. kötet 1‐6. o. 1958 január.

2Lásd: Hajós-Neukornm-Surányi: Matematikai Versenytételek II. rész. Tankönyvkiadó 1957, 57. o., 1937. évi 2. feladat.