Kezdőlap


Feladat:	878. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barnkopf Rudolf , Szodoray Erzsébet , Várallyay László
Füzet:	1958/november, 97 - 99. oldal		PDF \| MathML
Témakör(ök):	Poliéderek hasonlósága, Beírt gömb, Térfogat, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1958/január: 878. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Kössük össze a tetraéder beírt gömbjének $O$ középpontját a csúcsokkal, így négy új tetraéder keletkezik: $O B C D$ , $O C D A$ , $O D A B$ és $O A B C$ . Minthogy $O$ biztosan belső pontja a tetraédernek, azért az $O A B$ , $O A C$ , $O A D$ , $O B C$ , $O B D$ és $O C D$ háromszöglapok mentén való bevágással a tetraéder (mint tömör test) a négy új tetraéderre esik szét, és így $K$ köbtartalma e részek köbtartalmának összege. Kézenfekvő erre a célra a részek köbtartalmát úgy kifejezni, hogy alapnak mindig az $O$ -val szemben fekvő lapot vesszük; egyrészt, mert ezek az eredeti tetraéderrel közösek, másrészt mert így a magasság mindnégy résztestben ugyanaz, éspedig $ϱ$ . Így, az $A$ , $B$ , $C$ , ill. $D$ csúccsal szemben fekvő lapok területét $t_{1}$ , $t_{2}$ , $t_{3}$ , ill. $t_{4}$ -gyel jelölve

\begin{matrix} K = \frac{t_{1} ϱ}{3} + \frac{t_{2} ϱ}{3} + \frac{t_{3} ϱ}{3} + \frac{t_{4} ϱ}{3} . \end{matrix}

Fejezzük ki innen

ϱ

reciprokát

\begin{matrix} \frac{1}{ϱ} = \frac{t_{1}}{3 K} + \frac{t_{2}}{3 K} + \frac{t_{3}}{3 K} + \frac{t_{4}}{3 K} . \end{matrix}

(1)

A jobboldali hányadosokat a (felbontatlan) tetraéder köbtartalmának képlete alapján is kifejezhetjük a megfelelő magasságvonalak hosszával:

\begin{matrix} K = \frac{t_{i} m_{i}}{3} -ból \frac{t_{i}}{3 K} = \frac{1}{m_{i}}, (i = 1, 2, 3, 4) . \end{matrix}

(2)

Ezeket (1)-be behelyettesítve a b) összefüggést kapjuk. A c) összefüggés igazolása céljára kössük össze

A

B

C

D

-t a

B C D

lapot kívülről érintő gömb

O_{1}

középpontjával. Így ismét négy újabb tetraéderhez jutunk, ezekben

O_{1}

közös csúcs,

O_{1}

-gyel szemközt mindegyikben az eredeti tetraédernek egy lapja fekszik, és az

O_{1}

-ből kiinduló magasságvonal hossza mindegyikben

ϱ_{1}

. Mivel

O_{1}

B C D

lapnak az

A

-val ellentétes oldalán van, a többi három lapnak viszont ugyanazon az oldalán, mint az eredeti tetraéder megfelelő szemközti csúcsa, azért az

O_{1} B C D

és az

A B C D

tetraéderek együtt ugyanazt a teret töltik ki, mint a további bárom új tetraéder együtt. Ennek alapján az előzőkhöz hasonlóan:

\begin{matrix} K = \frac{t_{2} ϱ_{1}}{3} + \frac{t_{3} ϱ_{1}}{3} + \frac{t_{4} ϱ_{1}}{3} - \frac{t_{1} ϱ_{1}}{3}, \end{matrix}

majd

ϱ_{1}

reciprokát kifejezve:

\begin{matrix} \frac{1}{ϱ_{1}} = - \frac{t_{1}}{3 K} + \frac{t_{2}}{3 K} + \frac{t_{3}}{3 K} + \frac{t_{4}}{3 K}, \end{matrix}

és innen a (2) kifejezések helyettesítésével c) adódik.
A c)-hez hasonló további három összefüggés a következő

\begin{matrix} \frac{1}{ϱ_{2}} = \frac{1}{m_{1}} - \frac{1}{m_{2}} + \frac{1}{m_{3}} + \frac{1}{m_{4}}, & (3) \\ \frac{1}{ϱ_{3}} = \frac{1}{m_{1}} + \frac{1}{m_{2}} - \frac{1}{m_{3}} + \frac{1}{m_{4}}, \\ \frac{1}{ϱ_{4}} = \frac{1}{m_{1}} + \frac{1}{m_{2}} + \frac{1}{m_{3}} - \frac{1}{m_{4}} . \end{matrix}

Ezeket c)-vel összeadva, majd b) figyelembevételével

\begin{matrix} \frac{1}{ϱ_{1}} + \frac{1}{ϱ_{2}} + \frac{1}{ϱ_{3}} + \frac{1}{ϱ_{4}} = 2 (\frac{1}{m_{1}} + \frac{1}{m_{2}} + \frac{1}{m_{3}} + \frac{1}{m_{4}}) = \frac{2}{ϱ}, \end{matrix}

és evvel az a) összefüggést is igazoltuk.

Szodoray Erzsébet (Debrecen, Kossuth L. lg. IV. o. t.)

II. megoldás: A c) összefüggést így is igazolhatjuk: fektessünk a

B C D

lappal párhuzamos érintősíkot a

B C D

lapot kívülről érintő

O

közepű gömbhöz, és jelöljük e síknak az

A B

A C

A D

egyenesekkel való metszéspontjait sorra

B_{1}

C_{1}

D_{1}

-gyel (1. ábra).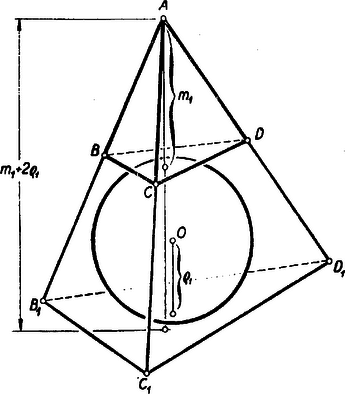

A kapott

A B_{1} C_{1} D_{1}

tetraéder nyilván hasonló az

A B C D

-hez, a

B_{1} C_{1} D_{1}

lapjához tartozó magassága

m_{1} + 2 ϱ_{1}

, végül az

O

gömb ennek beírt gömbje. Mivel a megfelelő hosszanti méretek aránya a hasonlóságból következően megegyezik, így

\begin{matrix} \frac{ϱ_{1}}{ϱ} = \frac{m_{1} + 2 ϱ_{1}}{m_{1}} = 1 + \frac{2 ϱ_{1}}{m_{1}}, \end{matrix}

és ebből

\begin{matrix} \frac{1}{ϱ_{1}} = \frac{1}{ϱ} - \frac{2}{m_{1}} . \end{matrix}

Itt a jobb oldalon a

b)

jobb oldalának behelyettesítése és összevonás után

c)

jobb oldalát kapjuk.

Várallyay László (Mosonmagyaróvár, Kossuth L. g. IV. o. t.)

Megjegyzés: A b) és c) összefüggés speciális esete egy a fentiekhez hasonlóan igazolható általánosabb összefüggésnek. Ismeretes, hogy ha az

A B C D

tetraéder belsejében levő tetszőleges

P

pont távolsága az

A

B

C

D

csúcsokkal szemközti lapoktól rendre

p_{a}

p_{b}

p_{c}

p_{d}

, továbbá az

A

B

C

D

csúcsokból kiinduló magasságvonalak hossza

m_{a}

m_{b}

m_{c}

m_{d}

, akkor

\begin{matrix} \frac{p_{a}}{m_{a}} + \frac{p_{b}}{m_{b}} + \frac{p_{c}}{m_{c}} + \frac{p_{d}}{m_{d}} = 1. \end{matrix}

Ha viszont

P

a tetraéderen kívül van, akkor minden olyan laptól vett távolsága, amelynek a tetraéderrel ellentétes oldalán helyezkedik el, az egyenlőségben negatív előjellel veendő (ilyen három is lehet; lásd K. M. L., 1(1947‐48), 123. oldal, 133. feladat). Az állítás könnyen bizonyítható résztetraéderekre bontással.
Írjuk fel ezt az összefüggést a beírt gömb középpontjára, majd a

B C D

lapot kívülről érintő gömb középpontjára. Ekkor

\begin{matrix} \frac{ϱ}{m_{1}} + \frac{ϱ}{m_{2}} + \frac{ϱ}{m_{3}} + \frac{ϱ}{m_{4}} = 1, ill. - \frac{ϱ_{1}}{m_{1}} + \frac{ϱ_{1}}{m_{2}} + \frac{ϱ_{1}}{m_{3}} + \frac{ϱ_{1}}{m_{4}} = 1, \end{matrix}

és innen

ϱ

, ill.

ϱ_{1}

-gyel való osztással b) ill. c) adódik.

Bärnkopf Rudolf (Bp. IX., József A. gépip. t. III. o. t.)