Kezdőlap


Feladat:	874. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Elbert Árpád , Győry Kálmán , Tamás Gyula
Füzet:	1958/november, 92 - 94. oldal		PDF \| MathML
Témakör(ök):	Húrsokszögek, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1958/január: 874. matematika feladat

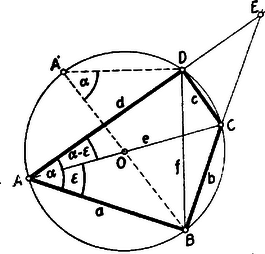
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Négyszögünk húrnégyszög, mert két szemben fekvő szögének összege $β + δ = 180^{\circ}$ , és a keresett $A C$ átló átmérője a körülírt körnek, mert $β$ és $δ$ ennek látószöge a $B$ , $D$ pontból. A további jelöléseket mindhárom megoldás céljára lásd az ábrán.

A C

átlót mint az adatokkal meghatározott

A B D

háromszög körülírt körének átmérőjét számítjuk az

A' B D

derékszögű háromszögből:

\begin{matrix} A C = 2 r = \frac{f}{sin α} = \frac{\sqrt[]{a^{2} + d^{2} - 2 a d cos α}}{sin α} . \end{matrix}

(1)

(Meg lehet mutatni, hogy a felhasznált összefüggés

α ≧ 90^{\circ}

esetén is érvényes.)

Elbert Árpád (Kaposvár, közg. t. IV. o. t.)

II. megoldás: Határozzuk meg először

A C

-nek

A B

-vel bezárt

ε

szögét. Az

A B C

és

A C D

derékszögű háromszögekből

\begin{matrix} A C = \frac{a}{cos ε} = \frac{d}{cos (α - ε)} . \end{matrix}

(2)

Innen a második nevezőt kifejtve rendezéssel olyan egyenletet kapunk, amelynek minden tagjában vagy

sin ε

vagy

cos ε

szerepel. Célszerű ilyenkor elsőnek

tg ε

-t kifejezni:

\begin{matrix} tg ε = \frac{d - a cos α}{a sin α} . \end{matrix}

(3)

Ebből a (2)-beli első kifejezés céljára:

\begin{matrix} \frac{1}{cos ε} = \sqrt[]{{tg}^{2} ε + 1} = \frac{\sqrt[]{{(d - a cos α)}^{2} + a^{2} sin^{2} α}}{a sin α} . \end{matrix}

(A négyzetgyök pozitívnak veendő, mert

ε

biztosan pozitív hegyesszög.) Ezt átalakítva, majd (2)-be beírva ismét (1)-re jutunk.

Győry Kálmán (Ózd, József Attila g. IV. o. t.)

III. megoldás: Négyszögünkre érvényes Ptolemaios tétele:

\begin{matrix} a c + b d = e f . \end{matrix}

Itt a

c

és

b

oldalakat Pythagoras tétele alapján

e

a

d

-vel kifejezve

e

-re ezt az egyenletet kapjuk:

\begin{matrix} a \sqrt[]{e^{2} - d^{2}} + d \sqrt[]{e^{2} - a^{2}} = e f . \end{matrix}

Az innen négyzetreemeléssel, rendezéssel és újabb négyzetreemeléssel adódó egyenlet egyetlen pozitív gyöke:

\begin{matrix} e = \frac{2 a d f}{\sqrt[]{4 a^{2} d^{2} - {(f^{2} - a^{2} - d^{2})}^{2}}}, \end{matrix}

és ez

f

-nek már használt kifejezése alapján ismét (1)-re vezet.

Tamás Gyula (Ózd, József Attila g. IIl. o. t.)

Megjegyzések: Minthogy nyilván konvex négyszögről van szó, azért az

A B D

és

C B D

háromszögek csak

A

- vagy

C

-nél lehetnek tompaszögűek. Eszerint a megoldhatóság két feltétele:

\begin{matrix} a cos a < d \end{matrix}

Az első feltétel teljesülésével a II. megoldás (3) részeredménye is pozitív lesz, és ugyanez áll a másodiknak a teljesülésével a (3)-ből

a

és

d

szerepének felcserélésével adódó

\begin{matrix} tg (α - ε) = \frac{a - d cos α}{d sin α} \end{matrix}

(3')

kifejezésre.

α \neq 90^{\circ}

esetén négyszögünk bármelyik szemközti oldalpár meghosszabbítása azaz egy (kisebb) derékszögű háromszög hozzácsatolása révén derékszögű háromszöggé egészíthető ki. Ennek

E

,,új'' csúcsánál levő szög

90^{\circ} - α

, ill.

α - 90^{\circ}

aszerint, hogy

α

hegyes, ill. tompa szög. Már most egymásután kifejezve az

A E

átfogót, kivonással, ill. összeadással a

B E

vagy

D E

befogót, végül a

C E

átfogót,

A C

A C E

háromszögből számítható. ‐ Az

α = 90^{\circ}

esetben pedig téglalap-számítássá egyszerűsödik a feladat.

Elbert Árpád koordinátageometriai megoldást is küldött be.