Kezdőlap


Feladat:	871. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Trón Lajos
Füzet:	1958/szeptember, 7 - 8. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1957/december: 871. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a szögfelezők és oldalak metszéspontjai $A_{1}$ , $B_{1}$ , $C_{1}$ , az $A B C$ háromszög területe 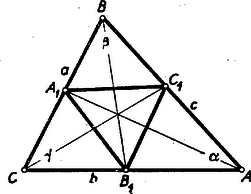$T$ .

Az ábráról leolvasható, hogy a kérdéses területet megkapjuk, ha az eredeti háromszög területéből levonjuk három kis háromszög területét:

\begin{matrix} t = T - t_{B_{1} A C_{1}} - t_{A_{1} B C_{1}} - t_{A_{1} C B_{1}} . \end{matrix}

Határozzuk meg a kivonandó területeket két-két oldal és a közbezárt szög segítségével:

\begin{matrix} t = T - \frac{B_{1} A \cdot A C_{1} sin α}{2} - \frac{A_{1} B \cdot B C_{1} sin β}{2} - \frac{A_{1} C \cdot C B_{1} sin γ}{2} . \end{matrix}

(1)

A szereplő távolságokat és szinuszokat az eredeti háromszög oldalaival kell kifejeznünk. A szögfelezők osztásaránya alapján:

\begin{matrix} B C_{1} & = \frac{a c}{a + b}, A C_{1} = \frac{b c}{a + b}, \\ B A_{1} & = \frac{a c}{b + c}, C A_{1} = \frac{a b}{b + c}, \\ A B_{1} & = \frac{b c}{a + c}, C B_{1} = \frac{a b}{a + c} . \end{matrix}

A már előbb is használt háromszög területképletből pedig

\begin{matrix} sin α = \frac{2 T}{b c}, sin β = \frac{2 T}{a c}, sin γ = \frac{2 T}{a b} . \end{matrix}

Az (1) képletbe helyettesítve, egyszerűsítve és közös nevezőre hozva:

\begin{matrix} t = T (1 - \frac{b c}{(a + b) (a + c)} - \frac{a c}{(a + b) (b + c)} - \frac{a b}{(a + c) (b + c)}) = \\ = T \cdot \frac{2 a b c}{(a + b) (b + c) (c + a)} . \end{matrix}

T

területet kifejezhetjük az oldalak segítségével a Heron-képlettel:

\begin{matrix} t = \frac{2 a b c \sqrt[]{s (s - a) (s - b) (s - c)}}{(a + b) (b + c) (c + a)} . \end{matrix}

Trón Lajos (Debrecen, Fazekas g. III. o. t.)