Kezdőlap


Feladat:	866. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Hajna János , Máthé Csaba , Sárközy András
Füzet:	1958/május, 147 - 150. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletek, Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1957/december: 866. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: a) Alkalmazzuk a

\begin{matrix} sin α + sin β = 2 sin \frac{α + β}{2} cos \frac{α - β}{2} összefüggést az α = 3 x és β = x \end{matrix}

szögekre:

\begin{matrix} sin 3 x + sin x = 2 sin 2 x cos x, \end{matrix}

s így az a) egyenlet a következő alakra hozható:

\begin{matrix} sin x + sin 2 x + sin 3 x = 2 sin 2 x cos x + sin 2 x = sin 2 x (2 cos x + 1) = 0. \end{matrix}

\begin{matrix} Ebből vagy & sin 2 x = 0, \\ 2 x = \pm k \cdot 180^{\circ} & (k = 0, 1, 2, 3, ...), \\ azaz & x = \pm k \cdot 90^{\circ}, \\ vagy & 2 cos x + 1 = 0, \\ cos x = - \frac{1}{2}, \\ s ekkor & x = 120^{\circ} \pm n \cdot 360^{\circ}, \\ illetve & x = 240^{\circ} \pm n \cdot 360^{\circ} . & (n = 1, 2, ...) \end{matrix}

Ezzel megtaláltuk az egyenlet összes gyökeit.
A b) esetben alkalmazzuk a

\begin{matrix} cos α + cos β = 2 cos \frac{α + β}{2} cos \frac{α - β}{2} \end{matrix}

összefüggést a

3 x

és

x

szögekre. Így az egyenlet a következő alakot ölti:

\begin{matrix} cos x + cos 2 x + cos 3 x = cos 2 x + 2 cos 2 x cos x = cos 2 x (1 + 2 cos x) = 0. \end{matrix}

Ez úgy állhat fenn, ha vagy az első, vagy a második tényező

0

. Első esetben

\begin{matrix} 2 x = & 90^{\circ} \pm n \cdot 180^{\circ}, \\ azaz & x = & 45^{\circ} \pm n \cdot 90^{\circ} & (n = 0, 1, 2, ...), \\ második esetben & x = & 120^{\circ} \pm n \cdot 360^{\circ} \\ vagy & x = & 240^{\circ} \pm n \cdot 360^{\circ} & (n = 0, 1, 2, ...) . \end{matrix}

Máthé Csaba (Győr, Révai g. II. o. t.)

II. megoldás: Arra kell törekednünk, hogy az egyenletben csak egyetlen szög szögfüggvénye szerepeljen. Ismeretes, hogy

\begin{matrix} sin 2 x = 2 sin x cos x . \end{matrix}

sin 3 x

értékét

x

szögfüggvényével kiszámíthatjuk:

\begin{matrix} sin 3 x = sin (2 x + x) = sin 2 x cos x + sin x cos 2 x = 2 sin x cos^{2} x + \\ + sin x (cos^{2} x - sin^{2} x) = sin x (3 cos^{2} x - sin^{2} x) = sin x (4 cos^{2} x - 1) . \end{matrix}

Ezeket az értékeket az a) egyenletbe helyettesítve:

\begin{matrix} sin x + sin 2 x + sin 3 x = sin x (1 + 2 cos x + 4 cos^{2} x - 1) = \end{matrix}

\begin{matrix} = 2 sin x cos x (1 + 2 cos x) = sin 2 x (1 + 2 cos x) = 0. \end{matrix}

Látható, hogy ugyanarra az egyenletre jutottunk, mint az I. megoldásban, ugyanazokat a gyököket kapjuk, mint ott.
b) A

\begin{matrix} cos 2 x = 1 - 2 sin^{2} x \end{matrix}

és a

\begin{matrix} cos 3 x = cos (2 x + x) = (1 - 2 sin^{2} x) cos x - 2 sin^{2} x cos x \end{matrix}

értékek behelyettesítésével egyenletünk a következőképpen alakul:

\begin{matrix} cos x + cos^{2} x + cos 3 x = (1 - 2 sin^{2} x) (1 + cos x) + cos x (1 - 2 sin^{2} x) = \\ = (1 - 2 sin^{2} x) (1 + 2 cos x) = cos 2 x (1 + 2 cos x) = 0. \end{matrix}

Az egyenlet egyezik az I. megoldásban kapott egyenlettel, ebből a gyököket ugyanúgy számíthatjuk ki, mint ott.

Hajna János (Pécs, Széchenyi g. II. o. t.)

III. megoldás: Az

O A

sugarú körben az

O A

szárból kiindulva mérjünk fel egymás után négyszer

x

középponti szöget, így kapjuk a körön az

A

B

C

D

E

pontokat (l. az ábrát).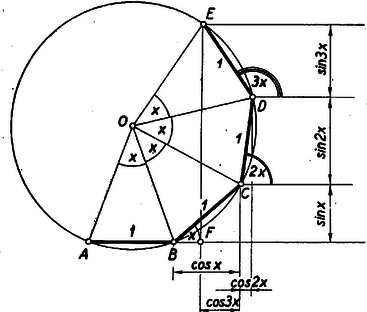

Válasszuk egységnek az

A B = B C = C D = D E

húrok hosszát. Ez megtehető, ha

x \neq n \cdot 360^{\circ} (n = 0, 1, 2, ...)

, ezeket az

x

értékeket egyenlőre zárjuk ki.
Az

A B

és

B C

egyenesek egymással bezárt egyik szöge

x

lesz (mert ha például az

O A B

és

O B C

egyenlő szárú háromszögek szögfelezőit az

O

csúcsból meghúzzuk, ezek szöge

x

lesz; a szögfelezők szögére merőleges szárú, említett szög szintén ugyanennyi). Ugyanígy a

C

pontban

2 x

, a

D

pontban pedig

3 x

nagyságú szög keletkezik.
Mivel a húrok egységnyi hosszúságúak, azért a

sin x

sin 2 x

és

sin 3 x

értékek az

A B

-re állított

E F

merőlegesen közvetlenül leolvashatóak, mégpedig könnyen ellenőrizhető, hogy (

x

értékétől függően) mindjárt előjelesen: ha valamelyik sinus negatív, értékét

E

-től lefelé kell mérnünk.
Így az

E F

szakasz hossza

sin x + sin 2 x + sin 3 x

. Ha tehát az a) egyenletet meg akarjuk oldani, azt kell csak vizsgálnunk, milyen

x

értékre lesz

E F

hossza nulla. Ez akkor következik be, ha

E \equiv A

vagy

E \equiv B

\begin{matrix} Első esetben & 4 x_{1} = \pm n \cdot 360^{\circ}, \\ azaz & x_{1} = \pm n \cdot 90^{\circ}, \\ második esetben & 3 x_{2} = 360^{\circ} \pm n \cdot 360^{\circ}, \\ vagyis & x_{2} = 120^{\circ} \pm n \cdot 120^{\circ} . \end{matrix}

A feladat elején kizártuk az

x = \pm n \cdot 360^{\circ}

szöget. Mivel azonban az a) egyenletnek ez nyilvánvalóan megoldása, a kapott két gyökcsoportban nem kell kizárnunk a

360^{\circ}

többszöröseit szolgáltató

n

-eket, vagyis

x_{1}

-nél is,

x_{2}

-nél is

\begin{matrix} n = 0, 1, 2, 3, ... \end{matrix}

‐ Ugyanígy belátható, hogy az

A B

meghosszabbításán a

cos x

cos 2 x

cos 3 x

értékeket kapjuk meg egymásután mérve előjelük szerint, s így

\begin{matrix} B F = cos x + cos 2 x + cos 3 x . \end{matrix}

A b) egyenlet olyan

x

-ekre teljesül, melyeknél

B \equiv F

. Ez akkor következik be, ha

E

B

ponttal esik össze, vagy ha a

B

-ben állított merőlegesnek a körrel való másik metszéspontjában van.

\begin{matrix} Első esetben & 3 x_{1} = \pm n \cdot 360^{\circ}, \\ tehát & x_{1} = \pm n \cdot 120^{\circ}, \\ második esetben & 4 x_{2} = 180^{\circ} \pm n \cdot 360^{\circ}, \\ x_{2} = 45^{\circ} \pm n \cdot 90^{\circ} . \end{matrix}

Mivel

x = \pm n

360^{\circ}

most nem megoldása a feladatnak, ki kell zárnunk az ilyen értékeket szolgáltató

n

-eket. Csak az első esetben kaphatnánk

360^{\circ}

többszörösét, így

x_{1}

-nél

n

3

-mal nem osztható, nem negatív egészeken fut végig,

x_{2}

esetében azonban tetszőleges nem negatív egész lehet.
‐ Összehasonlítással meggyőződhetünk róla, hogy ugyanazokat a gyököket kaptuk meg (rövidebb formába foglalva), mint az előző megoldásoknál.

Sárközy András (Gyöngyös, Vak Bottyán g. IV. o. t.)

Megjegyzés: A III. megoldásban követett gondolatmenet alapján megoldhatjuk a

\begin{matrix} sin x + sin 2 x + ... + sin k x = 0, \\ cos x + cos 2 x + ... + cos k x = 0 \end{matrix}

egyenleteket is, ahol

k

tetszőleges pozitív egész.