Kezdőlap


Feladat:	860. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Pál Gábor
Füzet:	1958/május, 140 - 141. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Számtani-mértani egyenlőtlenségek, Trapézok, Szélsőérték-feladatok differenciálszámítás nélkül, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1957/november: 860. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Jelöljük $x$ -szel az oldalfalnak az alapdeszkával bezárt hegyesszögét. A további jelöléseket az ábra mutatja.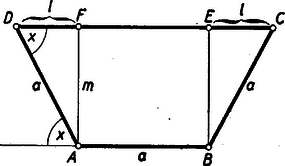

A F D

derékszögű háromszögből a trapéz magassága:

\begin{matrix} m = \sqrt[]{a^{2} - l^{2}}, \end{matrix}

így a trapéz területe

\begin{matrix} t = \frac{a + a + 2 l}{2} m = (a + l) \sqrt[]{a^{2} - l^{2}} . \end{matrix}

Mivel a terület mindig pozitív,

t

-nek (mint

l

függvényének) ugyanott van maximuma, ahol

3 t^{2}

-nek:

\begin{matrix} 3 t^{2} = 3 {(a + l)}^{2} (a^{2} - l^{2}) = (a + l) (a + l) (a + l) (3 a - 3 l) . \end{matrix}

A négy tényező összege

6 a

állandó. Így a számtani-mértani közép közti egyenlőtlenség alapján a szorzat akkor maximális, ha tényezői egyenlőek:

\begin{matrix} a + l = 3 a - 3 l, \end{matrix}

vagyis ha

\begin{matrix} l = \frac{a}{2} . \end{matrix}

A maximális csatorna-keresztmetszetet ez már meghatározza. Számítsuk ki, hogy a lehető legnagyobb trapéz terület esetén mekkora az

x

szög. Az

A F D

derékszögű háromszögből:

\begin{matrix} cos x = \frac{l}{a} . \end{matrix}

Ennek értéke a maximális területű trapéz esetén

\frac{\frac{a}{2}}{a} = \frac{1}{2}

, tehát

\begin{matrix} x = 60^{\circ} . \end{matrix}

A csatorna térfogata eszerint akkor lesz maximális, ha az oldalfal az alapdeszkával

x = 60^{\circ}

-os hegyesszöget zár be.

Pál Gábor (Miskolc, Kohászati techn. II. o. t.)

Megjegyzések: 1. Lényegében ugyanehhez a megoldáshoz jutunk, ha közvetlenül az alap és az oldallap közti

x

szöggel fejezzük ki a keresztmetszet területét. Ekkor

\begin{matrix} \begin{matrix} l = a cos x, & m = a sin x, \\ így \\ t = \frac{2 a + 2 l}{2} m = a^{2} (1 + cos x) sin x . \\ Ennek ugyanott van a maximuma, mint a \\ {(\frac{t}{a^{2}})}^{2} = {(1 + cos x)}^{2} sin^{2} x = {(1 + cos x)}^{2} (1 - cos^{2} x) = \\ = (1 + cos x) (1 + cos x) (1 + cos x) (1 - cos x) \end{matrix} \end{matrix}

függvénynek és ebből

3

-mal szorozva az előző megoldáshoz hasonlóan állapítható meg a maximum.
2. A feladatot megoldhatjuk differenciálszámítással is. Az ezzel a módszerrel történő megoldásokat szintén elfogadtuk.