Kezdőlap


Feladat:	858. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Elbert Árpád , Győry Kálmán , Katona Gyula , Meskó Attila , Sárközy András
Füzet:	1958/május, 135 - 138. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1957/november: 858. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A két szög összegének és különbségének sinusára ismeretes összefüggésből könnyen igazolható a következő azonosság:

\begin{matrix} 2 cos α sin β = sin (α + β) - sin (α - β) . \end{matrix}

Hogy a bizonyítandó egyenlőségre ezt alkalmazhassuk, szorozzuk meg a baloldal minden egyes tagját

2 sin \frac{π}{7}

-tel, s osszuk is el vele:

\begin{matrix} cos \frac{π}{7} + cos \frac{3 π}{7} + cos \frac{5 π}{7} = \\ = \frac{1}{2 sin \frac{π}{7}} (2 cos \frac{π}{7} sin \frac{π}{7} + 2 cos \frac{3 π}{7} sin \frac{π}{7} + 2 cos \frac{5 π}{7} sin \frac{π}{7}) = \\ = \frac{1}{2 sin \frac{π}{7}} [sin \frac{2 π}{7} + (sin \frac{4 π}{7} - sin \frac{2 π}{7}) + (sin \frac{6 π}{7} - sin \frac{4 π}{7})] = \\ = \frac{sin \frac{6 π}{7}}{2 sin \frac{π}{7}} = \frac{sin \frac{π}{7}}{2 sin \frac{π}{7}} = \frac{1}{2} . \end{matrix}

Ezzel a bizonyítandó összefüggést igazoltuk.

Meskó Attila (Bp. VII., Madách gimn. IV. o. t.)

II. megoldás: Tudjuk, hogy

cos α = - cos (π - α)

. Ezt az egyenlőség baloldalára alkalmazva:

\begin{matrix} cos \frac{π}{7} + cos \frac{3 π}{7} + cos \frac{5 π}{7} = - (cos \frac{6 π}{7} + cos \frac{4 π}{7} + cos \frac{2 π}{7}) . \end{matrix}

Ismeretes a következő összefüggés:

\begin{matrix} cos x + cos 2 x + ... + cos n x = \frac{sin \frac{x}{2} + sin (n + \frac{1}{2}) x}{2 sin \frac{x}{2}} - 1 = \frac{sin (n + \frac{1}{2}) x}{2 sin \frac{x}{2}} - \frac{1}{2} . \end{matrix}

(L. pl. Középiskolai Mat. Lapok XV. (1957.) 3‐4. sz., 69. oldal.) Behelyettesítve ide az

x = \frac{2 π}{7}

n = 3

értékeket, a bizonyítandó összefüggés baloldala tovább így alakul:

\begin{matrix} - (cos \frac{6 π}{7} + cos \frac{4 π}{7} + cos \frac{2 π}{7}) = - (\frac{sin \frac{7 π}{7}}{2 sin \frac{π}{7}}) - \frac{1}{2} . \end{matrix}

Mivel

sin \frac{7 π}{7} = sin π = 0

, így a vizsgált összeg értéke valóban

\frac{1}{2}

Sárközy András (Gyöngyös, Vak Bottyán g. IV. o. t.)

Megjegyzés: Ugyanezzel a gondolatmenettel belátható, hogy tetszőleges páratlan

n

esetén

\begin{matrix} cos \frac{π}{n} + cos \frac{3 π}{n} + cos \frac{5 π}{n} + ... + cos \frac{(n - 2) π}{n} = \frac{1}{2} . \end{matrix}

Elbert Árpád (Kaposvár, Közg. techn. IV. o. t.)

III. megoldás: Vegyünk fel egy egységnyi oldalú szabályos hétszöget s a hétszög köré írható kör középpontjából a csúcsokhoz húzott sugarakkal bontsuk háromszögekre. Húzzuk meg az

A_{1}

csúcsban a kör érintőjét, és rajzoljuk meg az egyes háromszögeknek a kör középpontjából induló magasságait (1. ábra).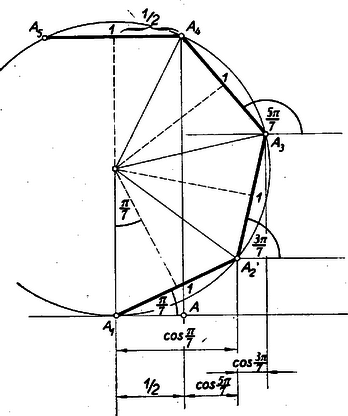

1. ábra

A magasságok az egyes háromszögek szögeit két-két

\frac{π}{7}

nagyságú szögre bontják. A körérintő az

A_{1}

pontban s az egységnyi hosszúságú

A_{1} A_{2}

oldal

\frac{π}{7}

nagyságú szöget zár be (hiszen szárai merőlegesek az egyik

O

-nál található

\frac{π}{7}

nagyságú szögre), az

A_{2}

pont vetítésével létrejövő derékszögű háromszögben az

A_{1}

csúcshoz tartozó befogó hossza

cos \frac{π}{7}

. Ugyanígy okoskodhatunk az

A_{2}

-nél levő

\frac{3 π}{7}

s az

A_{3}

csúcsnál lévő

\frac{5 π}{7}

szögeknél is. A kapott cosinus értékeket az érintőre vetítve (a

cos \frac{5 π}{7}

értéket negatív volta miatt mindjárt visszafelé mérve) az érintőn megkapjuk a

cos \frac{π}{7} + cos \frac{3 π}{7} + cos \frac{5 π}{7}

összeget. Az eredményül kapott

A_{1} A

szakasz hossza (az

A_{4} A_{5}

hétszögoldallal összemérve)

\frac{1}{2}

lesz, amivel épp a kívánt eredményt kaptuk.

Katona Gyula (Bp. VIII., Kandó híradásip. t. III. o. t.)

IV. megoldás: Rajzoljunk egységnyi oldalú szabályos hétszöget. Az

A_{1}

csúcsból vont átlók hossza legyen

a

és

b

. Az átlók az

A_{1}

csúcsnál rendre

\frac{π}{7}

nagyságú szögeket létesítenek (2. ábra).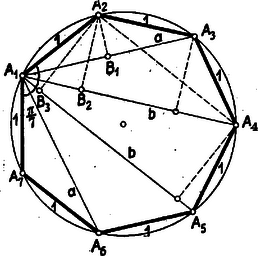

2. ábra

A_{2}

-ből bocsássunk merőlegest az első három átlóra, ezek talppontjai legyenek

B_{1}

B_{2}

B_{3}

. Így a létrejövő egységnyi átfogójú derékszögű háromszögekből

\begin{matrix} cos \frac{π}{7} = A_{1} B_{1}, cos \frac{2 π}{7} = - cos \frac{5 π}{7} = A_{1} B_{2}, cos \frac{3 π}{7} = A_{1} B_{3} . \end{matrix}

A_{1} B_{1}

oldal hossza

\frac{a}{2}

.
Az

A_{1} A_{2} A_{3} A_{4}

egyenlő szárú trapézból

\begin{matrix} A_{1} B_{2} = \frac{b - 1}{2} . \end{matrix}

A_{1} A_{2} A_{4} A_{5}

egyenlő szárú trapézból pedig

\begin{matrix} A_{1} B_{3} = \frac{b - a}{2} . \end{matrix}

Így

\begin{matrix} cos \frac{π}{7} + cos \frac{3 π}{7} + cos \frac{5 π}{7} = \frac{a}{2} + \frac{b - a}{2} - \frac{b - 1}{2} = \frac{1}{2} . \end{matrix}

Győry Kálmán (Ózd, József Attila g. IV. o. t.)