Kezdőlap


Feladat:	855. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Ágh A. , Arató P. , Bender Cecilia , Dániel G. , Detrekői Á. , Endrődy T. , Galambos J. , Grallert F. , Gyene A. , Győry Kálmán , Hank Zs. , Kisvölcsey J. , Kolonits F. , Kristóf L. , Leipniker P. , Losonczy L. , Majtényi S. , Makay Attila , Megyesi L. , Meskó A. , Montvay I. , Mózes E. , Ortutay M. , Pásztor Erzsébet , Pődör Bálint , S. Nagy Erzsébet , Sárközy A. , Simon L. , Szász D. , Szatmári G. , Szekér A. , Szodoray Erzsébet , Tatai P. , Tóth Zsuzsanna , Trón T.
Füzet:	1958/május, 129 - 132. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középpontos és egyéb hasonlósági transzformációk, Téglalapok, Feladat
Hivatkozás(ok):	Feladatok: 1957/október: 855. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Vegyünk fel a térben egy $N$ pontot, melynek a téglalap síkjára való vetülete $M$ . Tekintsük az $N$ pont, valamint az $A B C D$ téglalap által meghatározott gúlát (1. ábra).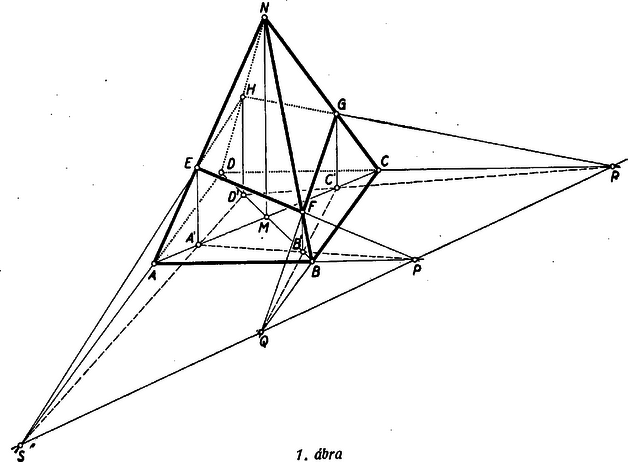

A' B'

, ill.

B' C'

egyeneseken át állítsunk az alapsíkra merőlegesen egy-egy síkot. Ezeknek a oldallapokkal való metszésvonalai az

E F

, ill.

F G

egyenesek lesznek, melyeknek az alapsíkkal való döféspontjai,

P

és

Q

meghatározzák az

E

F

és

G

pontokon átfektetett síknak az alapsíkkal való metszésvonalát. E metszésvonalnak, valamint a

D C

és

A D

egyeneseknek a metszéspontjai

R

és

S

. Mármost az

R G

egyenes benne van egyrészt a

D C N

oldallapnak a síkjában, másrészt az

E F G

síkban. Az előbbi miatt

R G

metszi

D N

oldalélt egy

H

pontban, melynek vetülete

D N

vetületén, a

D M

szakaszon van; az utóbbi pedig azt eredményezi, hogy az

E S

egyenes, mely benne van az

A D N

és

E F G

síkokban, szintén

H

-ban metszi a

D N

élt. (

D N

ugyanis az

A N D

és

C N D

síkok metszésvonala, ennek

E F G

síkkal csak egy közös pontja lehet.) Következésképpen

S E

merőleges vetülete,

S A'

átmegy

H

-nak

D'

vetületén, vagyis

C' R

és

A' S

valóban az

M D

szakaszon metszik egymást a

D'

pontban.
A szögszárak közötti párhuzamos szakaszokra vonatkozó arányossági tétel alapján:

\begin{matrix} \frac{N A}{N E} = \frac{M A}{M A'}, \end{matrix}

ebből

\begin{matrix} \frac{1}{N E} = \frac{M A}{N A \cdot M A'} . \end{matrix}

Hasonlóképpen:

\begin{matrix} \frac{1}{N F} = \frac{M B}{N B \cdot M B'}, \frac{1}{N G} = \frac{M C}{N C \cdot N C'}, \frac{1}{N H} = \frac{M D}{N D \cdot N D'} . \end{matrix}

Az 1957. évi Orsz. Mat. Tan. Verseny döntőjének 3. feladatában bizonyítottuk, hogy (Köz. Mat. Lapok XV. 1957. 1. sz., 10. o.):

\begin{matrix} \frac{1}{N E} + \frac{1}{N G} = \frac{1}{N F} + \frac{1}{N H} . \end{matrix}

(1)

Mivel

\begin{matrix} M A = M B = M C = M D \end{matrix}

és

\begin{matrix} N A = N B = N C = N D, \end{matrix}

a törtek kiszámított értékeit (1)-be beírva s az azonos számlálókkal s a nevezők azonos tényezőivel egyszerűsítve kapjuk, hogy

\begin{matrix} \frac{1}{M A'} + \frac{1}{M C'} = \frac{1}{M B'} + \frac{1}{M D'} . \end{matrix}

Győry Kálmán (Ózd, József A. g. IV. o. t.)

II. megoldás: A betűzést a 2. ábra mutatja.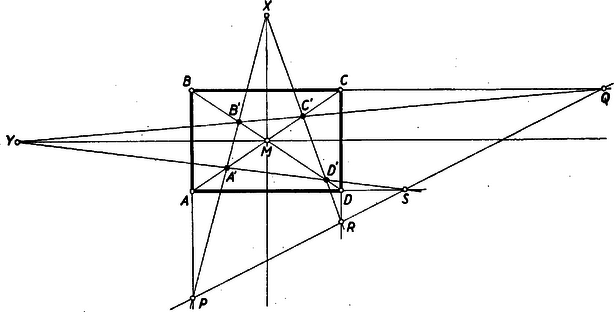

2. ábra

M

-ből

A B

-vel, ill.

B C

-vel párhuzamosan húzott egyenes messe

P B'

-t

X

-ben, ill.

Q B'

-t

Y

-ban. A

B B' P

és

M B' X

, továbbá a

B B' Q

és

M B' Y

háromszögek megfelelő szögei egyenlők, tehát ezek a háromszög párok hasonlóak. Az oldalak arányának egyenlősége azt adja, hogy a

B B' : M B'

, a

P B' : X B'

, és

Q B' : Y B'

arányok megegyeznek, az

X M Y

háromszög tehát egy

B'

középpontú hasonló transzformációval átvihető a

P B Q

háromszögbe, ahhoz tehát hasonló. Ekkor egyszersmind hasonló a

P A S

, az

R C Q

és az

R D S

háromszögekhez is és hasonló helyzetű is velük, tehát ezekbe is átvihető egy-egy alkalmas hasonlósági transzformációval. A

P A S

háromszögbe átvivő transzformáció középpontja az

A M

és

P X

egyenesek metszéspontja,

A'

; ezen a ponton tehát átmegy

S Y

is. Hasonlóan adódik, hogy

M C

és

Q Y

metszéspontján,

C

-n, átmegy

R X

is. Végül az

X M Y

háromszöget

R D S

-be átvivő hasonlósági transzformáció középpontja az

M D

és

R X

egyenesek

D'

metszéspontja, ezén tehát átmegy

S Y

is. Mivel

R X

, ill.

S Y

átmegy

C'

-n, ill.

A'

-n is, így

D'

, ami

M D

-n van rajt, az

A' S

és

C' R

egyenesek metszéspontja. Ezzel a feladat első állítását igazoltuk.
Az

A A' P

és

M A' X

háromszögek hasonlóságából

\begin{matrix} \frac{A M}{A' M} = \frac{A A' + A' M}{A' M} = \frac{A A'}{A' M} + 1 = \frac{P A}{M X} + 1. \end{matrix}

Hasonlóan

\begin{matrix} \frac{B M}{B' M} = \frac{P B}{M X} + 1, \frac{C M}{C' M} = \frac{R C}{M X} + 1, \frac{D M}{D' M} = \frac{R D}{M X} + 1. \end{matrix}

Így

\begin{matrix} \frac{A M}{A' M} + \frac{C M}{C' M} = \frac{P A + R C}{M X} + 2, \frac{B M}{B' M} + \frac{D M}{D' M} = \frac{P B + R D}{M X} + 2. \end{matrix}

A jobboldali törtek számlálói egyenlők, mert a

P A C R

, illetőleg

P B D R

trapézok párhuzamos oldalainak az összege áll a számlálókban. Ezek a középvonal kétszeresével egyenlők. A középvonal pedig az

A C

, ill.

B P

szárak közös

M

felezőpontjától a közös

P R

szárig terjed s így a két trapézban közös. Így a baloldali törtek összege egyenlő, ebből pedig

A M = B M = C M = D M

folytán következik a feladat második állítása is.

III. megoldás: Legyen

D'

R C'

és

M D

metszéspontja. Ha bebizonyítjuk, hogy

(A M A') (M D D') (D A S) = \frac{A A'}{A' M} \cdot \frac{M D'}{D' D} \cdot \frac{D S}{S A}

osztóviszony-szorzat értéke

(- 1)

, akkor a Menelaos-tétel megfordítása alapján

D'

rajta van az

S A'

egyenesen.
Írjuk fel részletesen a Menelaos-tételt az

A M B

háromszögre és

A' B'

szelőre,

M B C

háromszögre és

C' B'

szelőre, a

C M D

háromszögre és

C' D'

egyenesre:

\begin{matrix} \frac{A A'}{A' M} \cdot \frac{M B'}{B' B} \cdot \frac{B P}{P A} = - 1, & (1) \\ \frac{B B'}{B' M} \cdot \frac{M C'}{C' C} \cdot \frac{C Q}{Q B} = - 1, & (2) \\ \frac{C C'}{C' M} \cdot \frac{M D'}{D' D} \cdot \frac{D R}{R C} = - 1. & (3) \end{matrix}

Az 1. ábrán látható hasonló háromszögekből

\begin{matrix} \frac{B P}{P A} = \frac{C R}{R D} (= \frac{R C}{R D}), \end{matrix}

és

\begin{matrix} \frac{C Q}{Q B} = \frac{D S}{S A} \end{matrix}

Az elsőből

\frac{B P}{P A}

értékét írjuk be (1)-be, a másodikból

\frac{C Q}{Q B}

értékét (2)-be. Ha ezután az (1), (2), (3) egyenlőségeket összeszorozzuk, a jobboldalak szorzatában az egyszerűsítéseket rendre elvégezve épp a kívánt osztóviszony szorzatot kapjuk, a baloldal szorzata pedig

- 1

.
Ezzel a feladat első állítását igazoltuk. A továbbiak bizonyítása egyezik az I. megoldással.

Makay Attila (Bp. IX., Fáy g. IV. o. t.)

IV. megoldás: Ismét a feladat első részét bizonyítjuk.
Legyen

C' R

és

A' S

metszéspontja

D'

.
Az

A B C D

és az

A' B' C' D'

négyszögek megfelelő oldalainak metszéspontjai ‐ a feladat szerint ‐ egy egyenesen, az

S Q R P

egyenesen vannak.
Így a két négyszög között centrális kollineáció áll fenn (l. pl. a Kúpszeletek c. szakköri füzet 64. o.), a megfelelő csúcsokat összekötő egyenesek tehát egy ponton mennek át. Tehát

D D'

átmegy az

A A'

B B'

és

C C'

egyenesek

M

metszéspontján,

D'

rajta van az

M D

egyenesen.
A második rész egyezik az I. megoldással.

Pödör Bálint (Bp. II., Rákóczi g. IV. o. t.)