Kezdőlap


Feladat:	852. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Mihályffy László
Füzet:	1958/április, 108 - 110. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Egyenes körkúpok, Csonkakúp, Térfogat, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1957/október: 852. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Fejezzük ki először a feladatban szereplő térfogatok kiszámításához szükséges $A A'$ és $B B'$ szakaszokat a sugár és az $x$ segítségével.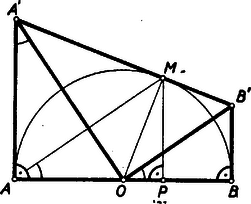
Az $O B B' M$ négyszög deltoid, mert két-két egymás mellett fekvő oldala egyenlő, és ezért $O B' ⊥ M B$ . Mivel azonban Thales-tétele értelmében $A M$ is merőleges $M B$ -re, így $O B' ∥ A M$ , azaz az egy ívvel jelzett szögek egyenlők.

A M P_{▵} \sim O B' B_{▵}

, mert két-két szögük egyenlő.
A hasonlóság miatt

\begin{matrix} A P : r = P M : B B', \end{matrix}

továbbá az ismert arányossági tétel alapján

P M = \sqrt[]{A P \cdot P B}

. E két eredményt egybevetve:

\begin{matrix} A P \cdot B B' = r \sqrt[]{A P \cdot P B} . \end{matrix}

Ebből

\begin{matrix} B B' = r \frac{\sqrt[]{A P \cdot P B}}{A P} = r \sqrt[]{\frac{P B}{A P}} = \frac{r}{\sqrt[]{x}} . \end{matrix}

A O M A'

négyszög ugyancsak deltoid és ezért

A M ⊥ O A'

. Így

A A' O ∢ = M A P ∢

, mert merőleges szárú szögek. Az

A O A'_{▵} \sim O B B'_{▵}

, mert két-két szögük egyenlő. A hasonlóság miatt

\begin{matrix} A A' : r = r : B B' . \end{matrix}

Innen

\begin{matrix} A A' = \frac{r^{2}}{B B'} = r \sqrt[]{x} . \end{matrix}

Ezek segítségével az

A B B' A'

trapéznak

A B

tengely körüli megforgatásakor keletkező csonkakúp térfogata a következőképpen írható fel:

\begin{matrix} V_{1} = \frac{2 r π}{3} (r^{2} x + r^{2} + \frac{r^{2}}{x}) = \frac{2 r^{3} π}{3 x} (x^{2} + x + 1) . \end{matrix}

A' O B'

háromszög

A B

tengely körüli forgatásakor keletkező forgástest térfogatát úgy számítjuk ki, hogy a

V_{1}

térfogatú csonkakúp térfogatából levonjuk az

A O A'

és az

O B B'

háromszögeknek az

A B

tengely körüli forgatásakor keletkező forgáskúpok

V_{3}

, ill.

V_{4}

térfogatát:

\begin{matrix} V_{2} = V_{1} - V_{3} - V_{4} = \frac{2 r^{3} π}{3 x} (x^{2} + x + 1) - \frac{r^{2} x π r}{3} - \frac{r^{2} π r}{3 x} = \\ = \frac{r^{3} π}{3 x} (2 x^{2} + 2 x + 2 - x^{2} - 1) = \frac{r^{2} π}{3 x} {(x + 1)}^{2} . \end{matrix}

Legyen tehát

\begin{matrix} \frac{V_{2}}{V_{1}} = \frac{{(x + 1)}^{2}}{2 (x^{2} + x + 1)} = m . \end{matrix}

Innen

\begin{matrix} (2 m - 1) x^{2} + 2 (m - 1) x + 2 m - 1 = 0. \end{matrix}

2 m - 1 \neq 0

, mert különben az egyenletből

x

0

lenne ‐ ez pedig a feladat szerint nem lehet. Így a másodfokú egyenlet oldóképletét használhatjuk.

2

-vel mindjárt egyszerűsítve

\begin{matrix} x_{1,2} = \frac{- (m - 1) \pm \sqrt[]{{(m - 1)}^{2} - {(2 m - 1)}^{2}}}{2 m - 1} = \frac{1 - m \pm \sqrt[]{m (2 - 3 m)}}{2 m - 1} . \end{matrix}

x

-re valós értéket kapunk, ha a diszkrimináns:

m (2 - 3 m) ≧ 0

, azaz

\begin{matrix} 0 ≦ m ≦ \frac{2}{3} . \end{matrix}

A feladat szerint

x

-nek pozitívnak is kell lennie. Egy tört akkor pozitív, ha számlálója-nevezője egyező előjelű. A számlálóból

1 - m

mindig pozitív, ha

0 ≦ m ≦ \frac{2}{3}

; a gyök alatt

{(m - 1)}^{2}

-nél ‐ ami ugyanannyi, mint

{(1 - m)}^{2}

‐, mindig kisebb szám áll. Ezek alapján a számláló mindig pozitív, kell tehát, hogy nevező is az legyen, ez pedig csak az

m > \frac{1}{2}

értékeknél következik be. Így végeredményben

m

-re a következő megszorítást kaptuk:

\begin{matrix} \frac{1}{2} < m ≦ \frac{2}{3} . \end{matrix}

Ebből azonnal látható, hogy

m

maximuma

\frac{2}{3}

.
Ha

m

maximális, akkor az

x

-re kapott képletben a diszkrimináns

0

, és

x = \frac{A P}{P B} = 1

M

vetülete tehát

O

-ban van, azaz

A' B' ∥ A B

. Ebben az esetben a trapézból téglalap lesz, a forgatáskor keletkezett forgástest pedig henger.

Mihályffy László (Szeged, Radnóti g. III. o. t)