Kezdőlap


Feladat:	850. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Pulay Péter
Füzet:	1958/április, 104 - 107. oldal		PDF \| MathML
Témakör(ök):	Beírt kör, Súlypont, Sokszögek súlypontjának koordinátái, Kör egyenlete, Szinusztétel alkalmazása, Háromszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1957/október: 850. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Helyezzük el a megszerkesztettnek képzelt derékszögű háromszöget egy koordináta rendszerben úgy, hogy a koordinátatengelyek egybeessenek a befogókkal; és hosszúság-egységnek vegyük az átfogót. A befogók hossza az egyik hegyesszög szögfüggvényével kifejezve $sin α$ és $c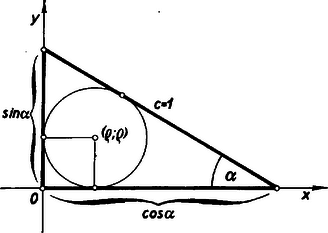os α$ (l. ábra).

1. ábra

Ha a beírható kör sugarát

ϱ

-val jelöljük, középpontjának mindkét koordinátája

ϱ

lesz, így a kör egyenlete:

\begin{matrix} {(x - ϱ)}^{2} + {(y - ϱ)}^{2} = ϱ^{2}, \end{matrix}

azaz

\begin{matrix} x^{2} + y^{2} - 2 ϱ (x + y) + ϱ^{2} = 0. \end{matrix}

(1)

A hegyesszögű csúcsokból a

ϱ

sugarú beírható körhöz húzható érintőszakaszok páronként egyenlőek, így a két befogón levő érintőszakaszok összege az átfogót adja:

\begin{matrix} (sin α - ϱ) + (cos α - ϱ) = 1, \end{matrix}

ebből

\begin{matrix} ϱ = \frac{sin α + cos α - 1}{2} . \end{matrix}

(2)

A súlypont koordinátái a háromszög csúcspontjainak koordinátáiból kiszámíthatóan

(\frac{cos α}{3}, \frac{sin α}{3})

. Ezek a feladat szerint kielégítik a beírható kör egyenletét.

ϱ

(2) alatti értékét, valamint a súlypont koordinátáit (1)-be helyettesítve a

sin^{2} α + cos^{2} α = 1

azonosság felhasználásával rendezés után a következő egyenletet kapjuk:

\begin{matrix} \frac{1}{9} - \frac{1}{3} (sin α + cos α - 1) (sin α + cos α) + {(\frac{sin α + cos α - 1}{2})}^{2} = 0. \end{matrix}

Jelöljük

(sin α + cos α)

-t

z

-vel, az egyenletet

36

-tal végigszorozva:

\begin{matrix} 4 - 12 (z - 1) z + 9 (z^{2} - 2 z + 1) = 0. \end{matrix}

Ebből

z

-re a következő másodfokú egyenletet kapjuk:

\begin{matrix} 3 z^{2} + 6 z - 13 = 0, \end{matrix}

z

-re csak a pozitív gyököt kell vennünk (hiszen

sin α

is,

cos α

is pozitívok):

\begin{matrix} z = \frac{- 6 + \sqrt[]{36 + 12 \cdot 13}}{6} = - 1 + \frac{\sqrt[]{48}}{3} = \frac{4 \sqrt[]{3}}{3} - 1. \end{matrix}

Tehát

\begin{matrix} sin α + cos α = \frac{4 \sqrt[]{3}}{3} - 1, \end{matrix}

mindkét oldal négyzetre emelésével

\begin{matrix} sin^{2} α + 2 sin α cos α + cos^{2} α = \frac{16}{3} - \frac{8 \sqrt[]{3}}{3} + 1, \end{matrix}

innen az ismert szögfüggvény-összefüggések felhasználásával

\begin{matrix} sin 2 α = \frac{16 - 8 \sqrt[]{3}}{3} \sim \frac{2, 1436}{3} = 0, 7145. \end{matrix}

A közelítő értéket visszakeresve

\begin{matrix} 2 α = 45^{\circ} 36' \underset{̲}{\underset{̲}{α = 22^{\circ} 18' .}} \end{matrix}

A másik szög

\begin{matrix} \underset{̲}{\underset{̲}{β = 67^{\circ} 12' .}} \end{matrix}

Ezzel a derékszögű háromszög szögeit meghatároztuk. Hátra van még a háromszög megszerkesztése. A beírható kör sugarára a feladat elején kapott összefüggésbe behelyettesíthetjük

sin α + cos α

kiszámított értékét:

\begin{matrix} ϱ = \frac{2 \sqrt[]{3}}{3} - 1 \end{matrix}

Ebből

ϱ

-t meg tudjuk szerkeszteni. A beírható kör sugara és az átfogó már egyértelműen meghatározzák a derékszögű háromszöget. A beírható kör

O

középpontja ugyanis rajt van egyrészt az átfogóval párhuzamosan

ϱ

távolságra haladó egyenesen, másrészt az átfogó és

O

által meghatározott háromszög két szögének összege

\frac{α}{2} + \frac{β}{2} = 45^{\circ}

, s így

O

az átfogóhoz tartozó

135^{\circ}

-os látószög-köríven is rajta van (2. ábra). (A látószögkör középpontja az átfogó felezőmerőlegesén

\frac{c}{2}

távolságra levő pont.)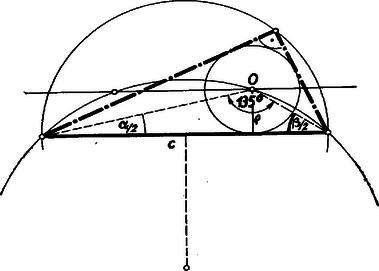

2. ábra

A beírt kör megrajzolása után érintőt szerkesztünk az átfogó végpontjaiból: ezek lesznek a derékszögű háromszög befogói. A feladatot most már teljesen megoldottuk.

II. megoldás: Jelöljük a megszerkesztendő

A B C

derékszögű háromszögben a beírt kör középpontját

O

-val, a súlypontot

S

-sel, az átfogó felezőpontját

F

-fel, a beírt kör sugara legyen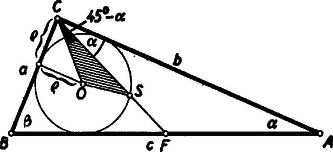

ϱ

(3. ábra).

3. ábra

Mivel

F

a háromszög köré írható (Thales-)kör középpontja, így az

A C F_{▵}

egyenlő szárú,

A

-nál és

C

-nél levő két szöge

α

. Az

O

középpont a derékszög szögfelezőjén van, tehát

O C S ∢ = 45^{\circ} - α

. A

C F

szakasz hossza az átfogó fele,

\frac{c}{2}

, a

C S

szakasz hossza ennek

\frac{2}{3}

-része, azaz

\frac{c}{3}

. A

C O S

háromszög

O S

oldala

ϱ

, a harmadik oldala,

O C

, egy

ϱ

befogójú, egyenlő szárú derékszögű háromszög átfogója, hossza tehát

ϱ \sqrt[]{2}

.
A

C O S

háromszögre a cosinus-tételt alkalmazva

\begin{matrix} ϱ^{2} = \frac{c^{2}}{9} + 2 ϱ^{2} - \frac{2 c ϱ \sqrt[]{2}}{3} cos (45^{\circ} - α) . \end{matrix}

Fejezzük ki ebből a

cos (45^{\circ} - α)

-t, mindjárt fölhasználva a két szög különbségének cosinusára vonatkozó összefüggést:

\begin{matrix} cos (45^{\circ} - α) = \frac{1}{\sqrt[]{2}} cos α + \frac{1}{\sqrt[]{2}} sin α = \frac{c^{2} + 9 ϱ^{2}}{6 c ϱ \sqrt[]{2}} . \end{matrix}

sin α = \frac{a}{c}

cos α = \frac{b}{c}

és a beírható körhöz húzott érintőszakaszok egyenlősége miatt

a + b = c + 2 ϱ

. Ezek fölhasználásával és

\frac{1}{c}

-vel mindjárt egyszerűsítve

\begin{matrix} c + 2 ϱ = \frac{c^{2} + 9 ϱ^{2}}{6 ϱ}, \end{matrix}

ebből a

ϱ

-ra kapott

\begin{matrix} 3 ϱ^{2} + 6 c ϱ - c^{2} = 0 \end{matrix}

másodfokú egyenlet megoldásával (elég a pozitív gyököt figyelembe vennünk)

\begin{matrix} ϱ = \frac{- 6 c + \sqrt[]{36 c^{2} + 12 c^{2}}}{6} = c (\frac{2 \sqrt[]{3}}{3} - 1) . \end{matrix}

cos (45^{\circ} - α)

-ra kapott (1) összefüggést átalakítva és a most nyert

ϱ

értéket behelyettesítve

\begin{matrix} cos (45^{\circ} - α) = \frac{c}{6 ϱ \sqrt[]{2}} + \frac{3 ϱ}{2 c \sqrt[]{2}} = \frac{c}{\sqrt[]{2} c (4 \sqrt[]{3} - 6)} + \frac{c (2 \sqrt[]{3} - 3)}{2 c \sqrt[]{2}} \approx 0, 9259. \end{matrix}

Ebből

\begin{matrix} 45^{\circ} - α = 22^{\circ} 12', \end{matrix}

\begin{matrix} \underset{̲}{\underset{̲}{α = 22^{\circ} 48' .}} \end{matrix}

A háromszög másik szöge akkor

\begin{matrix} \underset{̲}{\underset{̲}{β = 67^{\circ} 12' .}} \end{matrix}

A háromszög megszerkesztése a

ϱ

-ra kapott képlet felhasználásával, az átfogó ismeretében a következőképpen történhet. Először megszerkesztjük a

\frac{2 \sqrt[]{3}}{3} - 1

távolságot, aztán (pl. hasonlósággal) ennek

c

-szeresét.

ϱ

és az átfogó már meghatározzák a derékszögű háromszöget: megszerkesztését az előző megoldásban ismertettük.

Pulay Péter (Bp. I., Petőfi g. IV. o. t.)