Kezdőlap


Feladat:	849. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Fanta Katalin
Füzet:	1958/április, 103 - 104. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletek, Körülírt kör, Beírt kör, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1957/október: 849. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Fejezzük ki az $a$ , $b$ , $c$ oldalú háromszög területét először $ϱ$ -val és a félkerülettel, majd két oldal s a közbezárt szög segítségével:

\begin{matrix} T = ϱ \frac{a + b + c}{2} = \frac{b c sin α}{2} . \end{matrix}

Ebből

\begin{matrix} ϱ = \frac{b c sin α}{a + b + c} . \end{matrix}

Ismeretes, hogy az oldalak a szögek és a körülírt kör sugarának segítségével a következőképpen fejezhetők ki: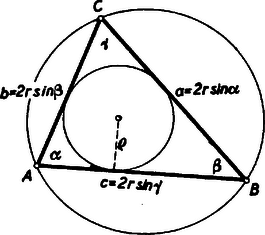

\begin{matrix} a = 2 r sin α, b = 2 r sin β, c = 2 r sin γ . \end{matrix}

Ezt a

ϱ

-ra kapott képletbe helyettesítve és

2 r

-rel egyszerűsítve :

\begin{matrix} ϱ = \frac{2 r sin α sin β sin γ}{sin α + sin β + sin γ} . \end{matrix}

(1)

A feladat szövegében adott értékek fölhasználásával számítsuk ki a szereplő sinusokat (mivel

α < 180^{\circ}

sin α

-ra elég a pozitív értéket venni) :

\begin{matrix} sin α = \frac{1}{\sqrt[]{{ctg}^{2} α + 1}} + \frac{1}{\sqrt[]{9 + 1}} = \frac{1}{\sqrt[]{10}} . \end{matrix}

sin γ = [180^{\circ} - (α + β)] = sin (α + β) = sin α cos β + cos α sin β

, ezt

sin β

-val végigszorozva és

sin β sin γ

értékét behelyettesítve :

\begin{matrix} \frac{1}{\sqrt[]{10}} = sin β (sin α cos β + \sqrt[]{1 - sin^{2} α} sin β)) = \frac{1}{\sqrt[]{10}} sin β cos β + \frac{3}{\sqrt[]{10}} sin^{2} β . \end{matrix}

(

cos α

-t

sin α

-val kifejezve, elegendő volt a pozitív gyököt venni, hiszen

tg α

pozitív, s így

α < 90^{\circ}

.)
Szorozzunk végig

\sqrt[]{10}

-zel, fejezzük ki

cos β

-t

sin β

-val. Az így kapott egyenletet négyzetre emelve kapjuk, hogy

\begin{matrix} sin^{2} β (1 - sin^{2} β) = 1 - sin^{2} β + 9 sin^{4} β, \end{matrix}

azaz a zárójelet felbontva és rendezve :

\begin{matrix} 10 sin^{4} β - 7 sin^{2} β + 1 = 0. \end{matrix}

Ebből

\begin{matrix} sin^{2} β_{1} = \frac{1}{2} és sin^{2} β_{2} = \frac{1}{5} . \end{matrix}

sin β

-ra csak a pozitív értéket kell vennünk :

\begin{matrix} sin β_{1} = \frac{1}{\sqrt[]{2}}, sin β_{2} = \frac{1}{\sqrt[]{5}} . \end{matrix}

A megadott

sin β sin γ = \frac{1}{\sqrt[]{10}}

összefüggésből

\begin{matrix} sin γ_{1} = \frac{1}{\sqrt[]{5}}, sin γ_{2} = \frac{1}{\sqrt[]{2}} . \end{matrix}

Mivel

ϱ

-nak az (1) alatt kifejezett értékében

sin β

és

sin γ

fölcserélhetők, elég csak az egyik kapott értékpárt behelyettesiteni. Így a kiszámított szögfüggvény-értékek fölhasználásával:

\begin{matrix} ϱ = 2 r \frac{\frac{1}{\sqrt[]{10}} \cdot \frac{1}{\sqrt[]{2}} \cdot \frac{1}{\sqrt[]{5}}}{\frac{1}{\sqrt[]{10}} + \frac{1}{\sqrt[]{2}} + \frac{1}{\sqrt[]{5}}} = \frac{\sqrt[]{10}}{(1 + \sqrt[]{2} + \sqrt[]{5}) 5} r (\sim 0, 136 r) . \end{matrix}

Fanta Katalin (Szombathely, Kanizsai Dorottya lg. IV. o. t.)