Feladat: 847. matematika feladat Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Galambos János ,  Kristóf László ,  Pásztor Erzsébet ,  Tatai Péter 
Füzet: 1958/március, 88 - 90. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai szerkesztések, Hiperbola, mint kúpszelet, Feladat
Hivatkozás(ok):Feladatok: 1957/szeptember: 847. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az aszimptoták metszéspontja a hiperbola középpontját adja, a megadott P ponttal egy szögtartományba eső szögfelező pedig a hiperbola fókuszainak tartó egyenese.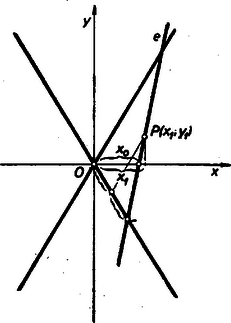
A P pontban a hiperbola érintőjét könnyen meg tudjuk rajzolni annak alapján, hogy P felezi az érintő aszimptoták közti szakaszát (1. az 1. ábrát).

 
 
1. ábra
 

Az aszimptoták és az érintő által bezárt háromszögnek meg tudjuk rajzolni a P-n áthaladó, egyik aszimptotával párhuzamos középvonalát, ez a másik aszimptotából a háromszögoldal felezőpontját metszi ki, abból pedig a háromszög csúcsát már megkaphatjuk. Ezt a pontot P-vel összekötve megszerkesztettük az érintőt.
Ha a koordinátarendszert a szokásos módon vesszük fel (origó az aszimptoták metszéspontja, fókuszok az X tengelyen), a P (x1, y1) pontban megszerkesztett érintő egyenlete:
xx1a2-yy1b2=1.

Az érintő X tengellyel való (xo,0) pontjának koordinátái kielégítik az egyenletet, behelyettesítve és a2-tel átszorozva:
x0x1=a2.
A hiperbola fél valós tengelyét tehát a két távolság mértani közepeként meg tudjuk szerkeszteni. Mivel az aszimptoták iránytangense ±ba, ezért az origóból a az X tengelyen a-t fölmérve, a kapott pontban állított merőlegesnek az aszimptotáig terjedő szakasza b lesz, az a, b befogójú derékszögű háromszög átfogója pedig c, a fókuszoknak az origótól való távolsága (hiszen a hiperbolánál a2+b2=c2). c ismeretében a két fókuszt már megszerkeszthetjük.
A feladatnak mindig van egy megoldása.
 

Pásztor Erzsébet (Makó, József A. g. IV. o. t.)
 

II. megoldás: Ismeretes,, hogy a hiperbola érintője felezi a ponthoz húzott vezérsugarak szögét. Rajzoljunk kört a hiperbola megszerkesztettnek képzelt F1, F2 fókuszain és a P ponton át (középpontja a képzetes tengelyen lesz rajta) (2. ábra).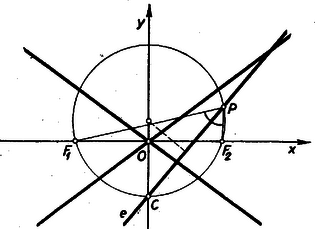
 
 
2. ábra
 

Messe a kört a P-ben húzott hiperbolaérintő a C pontban. Mivel CPF1∢=CPF2∢, azért C az F1F2 ív felezőpontja. Ez azt jelenti, hogy C rajta van F1F2 felezőmerőlegesén, ami nem más, mint a hiperbola képzetes tengelye.
A mondottak alapján a szerkesztés menete a következő lesz. Az előző megoldásban ismertetett módszerrel meg tudjuk szerkeszteni a hiperbola P-beli érintőjét, az aszimptoták szögfelezői pedig megadják a hiperbola tengelyeit. Az érintőn keletkezett PC szakasz felezőmerőlegese kimetszi az F1F2 fókuszokon, C-n és P-n áthaladó kör középpontját. A kört megrajzolva tehát a valós tengelyen megkapjuk a fókuszokat.
‐ Ha a P pont a valós nagytengelyre esik, akkor a fókuszokon és P-n át nem rajzolhatunk kört (a P-beli érintő sem metszi a képzetes tengelyt). Viszont ekkor P a hiperbola csúcsa, vagyis ismerjük a valós tengely felét, a-t; abból pedig ‐ mint az I. megoldásban láttuk ‐ már meg tudjuk szerkeszteni a fókuszokat.
 

Galambos János (Veszprém, Lovassy g. IV. o. t.)

III. megoldás: Ismeretes, hogy a fókuszpontokon átmenő tetszőleges körnek az aszimptotákkal való metszéspontjait összekötve, hiperbolaérintőt kapunk, és fordítva: minden érintőhöz szerkeszthetünk egy, a fókuszpontokon s az érintőnek az aszimptotákkal való metszéspontjain átmenő kört. (L. pl. a Kúpszeletek c. szakköri füzetet, 86. o.)
A fókuszok megszerkesztését ennek alapján úgy végezhetjük el, hogy először megszerkesztjük P-ben az érintőt, az érintőnek az aszimptoták közti szakasza a keresett körnek húrja lesz (3. ábra).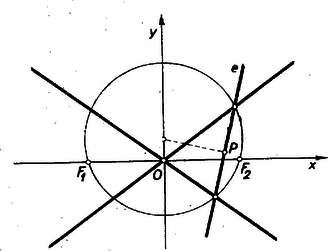
 
 
3. ábra
 

A kör középpontja rajta van egyrészt a húr felezőmerőlegesén, másrészt az F1F2 szakasz felező merőlegesén, vagyis a képzetes tengelyen. Az így kapott középpontból az érintő és az aszimptoták metszéspontjain át húzott kör kimetszi a fókuszokat.
 

Kristóf László (Mosonmagyaróvár, Kossuth g. IV. o. t.)
 

IV. megoldás: Tudjuk, hogy a hiperbola bármely pontjából az aszimptotákhoz húzott merőleges szakaszok szorzata állandó.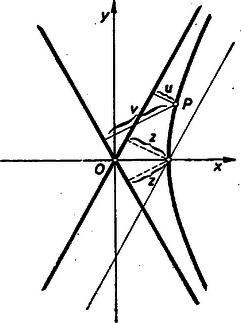
 
 
4. ábra
 

Legyen a P pont távolsága az aszimptotáktól u és v, a hiperbola csúcspontjának távolsága az aszimptotáktól z, akkor az előbb tett megjegyzésünk alapján
uv=z2.

Minthogy u és v adott, z mint mértani közép megszerkeszthető. Bármelyik aszimptotával z távolságban húzott párhuzamos a valós tengelyen kimetszi a hiperbola csúcsát. Ennek a középponttól való távolsága a, ennek ismeretében (mint az I. megoldásban láttuk) a középpont és fókuszpont c távolsága már megszerkeszthető.
 

Tatai Péter (Bp. XIV., I. István g. III. o. t.)
 

Megjegyzés: A feladatra újabb megoldási lehetőséget ad az a tétel, hogy a P ponton át a valós tengelyre húzott merőlegesnek az aszimptoták közti két szakasza a képzetes tengely felének, b-nek mértani közepe (1. pl. a Kúpszeletek c. szakköri füzet 84. o. A 85. oldalon pedig a-ra közölt összefüggés hasonló szerkesztési eljárást ad meg).