Kezdőlap


Feladat:	846. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Makay Attila , Szász Domokos
Füzet:	1958/március, 86 - 88. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai szerkesztések, Hiperbola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1957/szeptember: 846. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A hiperbolát tekinthetjük úgy is, mint azon körök középpontjainak mértani helyét, amelyek átmennek az egyik (pl. az $F_{2}$ ) gyújtóponton s érintik a másik gyújtópont ( $F_{1}$ ) körül rajzolt $2 a$ sugarú $k$ kört (az ún. vezérkört vagy iránykört). E körök közül keressük azokat, melyeknek középpontja az adott $e$ egyenesen van. Mivel az $e$ egyenes egy ilyen körnek átmérője, a keresett kör nemcsak az $F_{2}$ fókuszon, hanem a fókusz $e$ -re való tükörképén, $F'_{2}$ -n is átmegy. Az $e$ egyenes és a hiperbola metszéspontjainak megkeresése tehát olyan körök középpontjainak a megszerkesztését jelenti, amelyek átmennek két ponton, $F_{2}$ -n és $F'_{2}$ -n, azonkívül érintik az $F_{1}$ középpontú $k$ iránykört. Ezt a következőképpen végezhetjük el.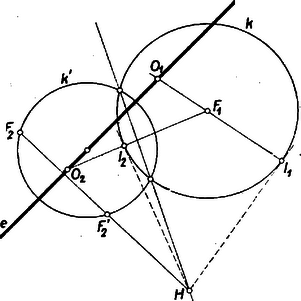
A megszerkesztendő kör és a $k$ iránykör hatványvonala a közös érintő, ennek pontjaiból ugyanolyan nagyságú érintőszakasz húzható mindkét körhöz. Mivel az $F_{2}$ -n és $F'_{2}$ -n átmenő körsor $F_{2} F'_{2}$ hatványvonalának ( $F_{2} F'_{2}$ a kívüli) pontjaiból a körsor minden eleméhez ugyanakkora nagyságú érintő húzható, így a közös érintő s az $F_{2} F'_{2}$ egyenes $H$ metszéspontja olyan pont lesz, amelyből az iránykörhöz és az $F_{2}$ és $F'_{2}$ pontokon átmenő körökhöz is azonos nagyságú érintő húzható. Így e körök bármelyikének és $k$ -nak a hatványvonala is átmegy $H$ -n. Ennek alapján a $H$ pont megszerkesztése úgy történhet, hogy megrajzoljuk a körsor egy tetszőleges $k'$ -körét, pl. olyant, amely metszi az iránykört (1. ábra).

1. ábra

A kapott metszéspontokat összekötő hatványvonal és az

F_{2} F_{2}'

hatványvonal metszéspontja lesz

H

. Innen az iránykörhöz húzható érintők

I_{1}

és

I_{2}

érintési pontjai a keresett hiperbolapontok (az

O_{1}

és

O_{2}

körközéppontok) ún. iránypontjai, s mint ismeretes, az

e

egyenesen levő

O_{1}

és

O_{2}

pontokat az

I_{1} F_{1}

és

I_{2} F_{2}

egyenesek metszik ki.
Ezzel a hiperbola és egyenes

O_{1}

és

O_{2}

metszéspontjait megszerkesztettük.
Ha az

e

egyenes átmegy az

F_{1}

fókuszon, akkor az

F_{2} F'_{2}

egyenes s a

k'

és

k

kör hatványvonalai nem metszik egymást. Ilyenkor az

F_{2}

-ben megrajzolt iránykörrel kell megoldanunk a feladatot. ‐ Ha pedig mindkét fókuszon átmegy az

e

egyenes, akkor a hiperbola csúcspontjait kell megszerkesztenünk: ezek az

F_{1} F_{2}

szakasz felezőpontjától

a

távolságnyira vannak az

e

egyenesen.
A feladatnak 2, 1 vagy 0 megoldása lehetséges. Ha a gyújtópontnak az egyenesre vonatkozó tükörképe az iránykörön kívül fekszik, két metszéspont van, ha rajta, akkor csak egy s az egyenes érintő. Ha pedig a tükörkép az iránykörnek belső pontja, akkor nincs metszéspont, mert hiszen nem létezik olyan kör, amely érinti az iránykört s egyszerre átmegy egy külső és egy belső pontján.

Makay Attila (Bp. IX., Fáy g. IV. o. t.)

II. megoldás: A hiperbola olyan pontok mértani helyének is tekinthető, amelyeknek egy ponttól (az egyik fókusztól) és egy egyenestől (a fókuszhoz tartozó vezéregyenestől) mért távolságai aránya állandó

\frac{c}{a}

érték (

a

a fél valós tengely hossza,

c

a fókuszok távolsága a középponttól).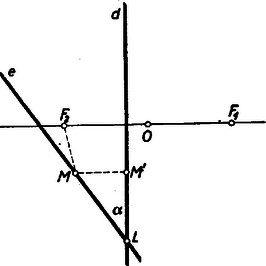

2. ábra

A 2. ábrán megrajzoltuk a hiperbola

F_{2}

fókuszhoz tartozó vezéregyenesét. (Ennek megszerkesztése történhet annak felhasználásával, hogy a vezéregyenesnek a középponttól való távolsága

t = \frac{a^{2}}{c}

: tehát megszerkeszthető pl. a

t : a = a : c

aránypár megoldásaként). Legyen az

e

és

d

egyenesek metszéspontja

L

, egymással bezárt szögük

α

, a hiperbolának

e

-vel való metszéspontja

M

, ennek merőleges vetülete a vezéregyenesen

M'

.
A kapott derékszögű háromszögből

\begin{matrix} \frac{M M'}{M L} = sin α, \end{matrix}

a vezéregyenes definíciójából:

\begin{matrix} \frac{F_{2} M}{M M'} = \frac{c}{a} . \end{matrix}

A kettőt összeszorozva:

\begin{matrix} \frac{F_{2} M}{M L} = \frac{c}{a} sin α . \end{matrix}

M

pont

L

-től és

F_{2}

-töl mért távolságainak aránya tehát állandó. Ez azt jelenti, hogy az

M

rajta van az

F_{2}

és

L

pontokhoz tartozó,

\frac{c}{a} sin α

arányú a Apollonius-körön. A kör megrajzolásával

M

-et meg tudjuk szerkeszteni.

2

1

vagy

0

a megoldások száma, aszerint, hogy az Apollonius-kör metszi, érinti vagy nem metszi az

e

egyenest.

Szász Domokos (Bp. V., Eötvös g. III. o. t.)

Megjegyzések: 1. A feladat megoldása történhet még körre való inverzióval, vagy ábrázoló geometriai úton, kúp és egyenes metszéspontjainak meghatározásával.
2. A feladatban felhasználtak (a hiperbola mint kétféle mértani hely, vezéregyenes, körsorok, hatványvonal stb.) megtalálhatók a Kúpszeletek c. szakköri füzetben, a megfelelő fejezetekben.