Kezdőlap


Feladat:	844. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dániel Gábor , Nagy Judit
Füzet:	1958/március, 83 - 85. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletek, Paraméteres egyenletek, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1957/szeptember: 844. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A feladatunk az, hogy olyan összefüggést állítsunk fel $a$ és az adott $a$ , $b$ és $r$ között, amelyből $α$ -t ki tudjuk számítani. Ezt a következőképpen érhetjük el.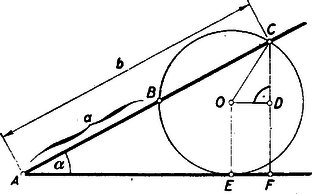
Rajzoljuk meg az $A$ csúcsú szöget és az $O$ középpontú kört (1. ábra), s vetítsük a metsző szögszár $A$ -tól távolabbi $C$ metszéspontját az érintő szögszárra, a kör középpontját pedig a $C F$ vetítősugárra és az érintőre.

1. ábra

A E

érintőszakasz mértani közepe az

A

-ból húzott szelő

a

és

b

szakaszainak:

A E = \sqrt[]{a b}

.
Számítsuk ki az

A C F

derékszögű háromszög oldalait:

\begin{matrix} A F = b cos α, C F = b sin α . \end{matrix}

Ezek alapján az

O C D

derékszögű háromszög oldalai:

\begin{matrix} O C = r, O D = b cos α - \sqrt[]{a b}, C D = b sin α - r . \end{matrix}

Írjuk fel erre a háromszögre a Pythagoras-tételt s akkor máris megkaptunk egy alkalmas összefüggést

α

és az adatok közt:

\begin{matrix} {(b sin α - r)}^{2} + {(b cos α - \sqrt[]{a b})}^{2} = r^{2}, \end{matrix}

a baloldalt tagokra bontva és rendezve:

\begin{matrix} b^{2} sin^{2} α - 2 b r sin α + r^{2} + b^{2} cos^{2} α - 2 b \sqrt[]{a b} cos α + a b = r^{2}, \\ b^{2} + a b - 2 b (r sin α + \sqrt[]{a b} cos α) = 0. \end{matrix}

b^{2}

-es tagok összevonásakor felhasználtuk azt, hogy

sin^{2} α + cos^{2} α = 1

.)
Egyszerűsíthetünk

b

-vel. Fejezzük ki

cos α

-t

sin α

segítségével és rendezzük az egyenletet:

\begin{matrix} \sqrt[]{a b} \sqrt[]{1 - sin^{2} α} = \frac{a + b}{2} - r sin α . \end{matrix}

Ebből mindkét oldal négyzetreemelésével

\begin{matrix} (r^{2} + a b) sin^{2} α - r (a + b) sin α + \frac{{(a - b)}^{2}}{4} = 0. \end{matrix}

Innen

\begin{matrix} {(sin α)}_{1,2} = \frac{r (a + b) \pm \sqrt[]{r^{2} {(a + b)}^{2} - (r^{2} + a b) {(a - b)}^{2}}}{2 (r^{2} + a b)} = \\ = \frac{r (a + b) \pm \sqrt[]{4 a b r^{2} - a b {(a - b)}^{2}}}{2 (r^{2} + a b)} . \end{matrix}

A kapott érték visszakeresésével ebből

α

-ra általában 2 értéket nyerünk.
Könnyen ellenőrizhető, hogy a feladat ugyanígy megoldható s az itt kapott eredményre vezet akkor is, ha a kör középpontja a szögszárakon kívül van, vagy ha a szög tompaszög.

Dániel Gábor (Bp. Vlll., Piarista g. III. o. t.)

II. megoldás: Legyen a szög csúcsát a kör középpontjával összekötő

O A

egyenesnek a szögszárakkal bezárt két szöge

α_{1}

és

α_{2}

, akkor a keresett

α

szögre vagy

α = α_{2} - α_{1}

, vagy

α = α_{2} + α_{1}

aszerint, hogy

O

a szögszárakon kívül vagy köztük van-e.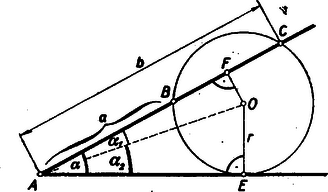

2. ábra

α_{2}

szögre az

A O E

derékszögű háromszögből (2. ábra)

\begin{matrix} tg α_{2} = \frac{O E}{A E} = \frac{r}{\sqrt[]{a b}}, \end{matrix}

ebből

α_{2}

-t már visszakereshetjük.
Az

α_{1}

szöget az

A O F

derékszögű háromszögből határozhatjuk meg, ahol

F

O

pont vetülete a metsző szögszáron. A háromszög egyik befogója

\begin{matrix} A F = a + \frac{b - a}{2} = \frac{b + a}{2} . \end{matrix}

A O

átfogót az

A O E

derékszögű háromszögből számíthatjuk ki:

\begin{matrix} A O = \sqrt[]{r^{2} + a b} . \end{matrix}

Így

\begin{matrix} cos α_{1} = \frac{a + b}{2 \sqrt[]{r^{2} + a b}} . \end{matrix}

α_{1}

-et ebből kell visszakeresnünk.
A keresett szög ezek alapján

\begin{matrix} α = arc tg \frac{r}{\sqrt[]{a b}} \pm arc cos \frac{a + b}{\sqrt[]{r^{2} + a b}} . \end{matrix}

A megoldás hegyes- és tompaszögre egyaránt vonatkozik.

Nagy Judit (Szombathely, Kanizsai D. Ig. III. o. t.)