Kezdőlap


Feladat:	836. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Argay Gy. , Borsi L. , Csanak Gy. , Endrődy T. , Frivaldszky S. , Galambos J. , Gyene A. , Győry K. , Hank Zs. , Horváth M. , Horváth Miklós , Király E. , Kolonits F. , Kristóf L. , Leipniker P. , Licskó L. , Makay A. , Mályusz K. , Megyesi L. , Molnár J. , Montvay I. , Németh József , Papp K. , Pásztor Erzsébet , Pulay P. , Pödör B. , Rockenbauer A. , Sárközy A. , Schipp F. , Simon L. , Solt Gy. , Staar Katalin , Stahl J. , Szász D. , Szatmáry Z. , Tatai P. , Tóth Zsuzsanna , Trón T. , Wollner R.
Füzet:	1958/február, 51 - 53. oldal		PDF \| MathML
Témakör(ök):	Két pont távolsága, szakasz hosszúsága, Síkgeometriai szerkesztések, Ellipszis, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1957/május: 836. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A feladatot koordináta-geometria segítségével oldjuk meg. Legyen az adott $r$ sugarú kör $O$ középpontja a koordinátarendszer kezdőpontja, az adott egyenes pedig az $X$ tengely. Az adott $P$ pont koordinátái legyenek $(u, v)$ , a körön levő $Q$ ponté $(x_{1}, y_{1})$ , akkor $Q$ pont vetületének, $Q'$ -nek koordinátái ( $x_{1}$ , 0). Mivel $Q$ rajta van a körön, kielégíti az egyenletét:

\begin{matrix} x_{1}^{2} + y_{1}^{2} = r^{2}, \end{matrix}

(1)

s mivel

P Q' = Q Q'

, így

\begin{matrix} {(u - x_{1})}^{2} + v^{2} = y_{1}^{2} . \end{matrix}

(2)

(1)-ből

y_{1}^{2}

-et kifejezve és (2)-be helyettesítve rendezzük, majd oldjuk meg az

x_{1}

-re kapott másodfokú egyenletet:

\begin{matrix} u^{2} - 2 u x_{1} + x_{1}^{2} + v^{2} = r^{2} - x_{1}^{2}, \\ 2 x_{1}^{2} - 2 u x_{1} + u^{2} + v^{2} - r^{2} = 0, \\ x_{1} = \frac{2 u \pm \sqrt[]{4 u^{2} - 8 (u^{2} + v^{2} - r^{2})}}{4} = \frac{u}{2} \pm \frac{1}{2} \sqrt[]{2 r^{2} - 2 v^{2} + u^{2}} . \end{matrix}

x_{1}

távolság (és segítségével

Q

pont) ebből már megszerkeszthető a Pythagoras-tétel segítségével.
A feladat megoldható, ha az

x_{1}

-re kapott kifejezésben a gyök alatti kifejezés nem negatív:

\begin{matrix} 2 r^{2} - 2 v^{2} - u^{2} \geq 0, \end{matrix}

vagyis ‐

2 r^{2}

-tel osztva

\begin{matrix} \frac{u^{2}}{2 r^{2}} + \frac{v^{2}}{r^{2}} \leq 1. \end{matrix}

Ebből kiolvasható, hogy azok az (

u

v

) koordinátájú pontok, melyeknél a szerkesztés elvégezhető, egy olyan középponti helyzetű, koordináta tengelyekkel egybeeső tengelyű ellipszis kerületén és belsejében helyezkednek el, melynek fél nagytengelye

r \sqrt[]{2}

, fél kistengelye pedig

r

.
A megoldások száma

x_{1}

-re 2, 1 vagy 0, aszerint, hogy az

x_{1}

-re kapott másodfokú egyenlet diszkriminánsa pozitív, nulla vagy negatív, tehát aszerint, hogy

P

az ellipszis belsejében, kerületén vagy kívüle helyezkedik el. Egy

x_{1}

-hez két

y_{1}

érték tartozik, tehát a

P

ponthoz szerkeszthető

Q

pontok száma 4, 2 vagy 0 (egy-egy tükrös az

X

tengelyre).

Horváth Miklós (Kaposvár, Táncsics g. III. o. t.)

II. megoldás: Tekintsük a feladatot megoldottnak (l. az ábrát).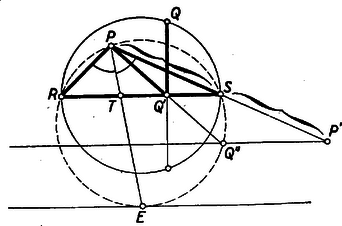

S Q R

derékszögű háromszögben a

Q Q'

magasság mértani közepe az átfogón létesített szeleteknek:

\begin{matrix} {(Q Q')}^{2} = R Q' \cdot Q' S . \end{matrix}

Mivel a feladat szerint

P Q' = Q Q'

, ezért

\begin{matrix} {(P Q')}^{2} = R Q' \cdot Q' S . \end{matrix}

(1)

Rajzoljunk

P R S_{Δ}

köré kört. (Ez mindig megtehető, ha

P

R

S

háromszöget határoznak meg; ha viszont

P

R S

átmérőn van rajt, a

Q

pont szerkesztése egyszerű, hiszen akkor

P

Q'

Q

45^{\circ}

-os, egyenlő szárú derékszögű háromszöget határoznak meg.) A

P Q'

egyenes messe ezt a kört a

Q''

pontban. A húrok szeleteire vonatkozó tétel szerint:

\begin{matrix} R Q' \cdot Q' S = P Q' \cdot Q' Q'' . \end{matrix}

Ezt (1)-gyel összehasonlítva látható, hogy

\begin{matrix} Q' Q'' = P Q' . \end{matrix}

Ennek alapján a szerkesztés a következő. Először a

P R S

háromszög köré írt körön a

Q''

-t szerkesztjük meg pl. úgy, hogy a

P S

szakasz meghosszabbítására

S

-ből fölmérjük a

P S

távolságot, a kapott pontból az

R S

oldallal húzott párhuzamos kimetszi a

Q''

pontot. Ezt

P

-vel összekötve az

R S

átmérőn megszerkesztettük a

Q'

pontot. Az abban emelt merőleges metszi ki a körből a

Q

gyanánt megfelelő pontokat.
A szerkesztés helyességét az előbbi gondolatmenet megfordításával igazolhatjuk.
Egy

P

ponthoz négy megoldást kapunk, ha az

R S

-sel párhuzamos egyenes két pontban metszi a kört, kettőt, ha érinti (hiszen egy megoldásként kapott

Q

ponttal együtt az

R S

átmérőre való tükörképe is megoldása a feladatnak). Nincs megoldás, ha nem metszi.
Vizsgáljuk meg, milyen

P

pontokra van megoldása a feladatnak. Megoldást akkor kapunk, ha az

R S

-sel húzott párhuzamos legalább érinti a kört. Mivel az

R S

-sel párhuzamos érintő

E

érintési pontja az

R P S ∢

szögfelezőjének a körrel való metszéspontja, így a párhuzamos olyan

P

pont esetén érint, amelyre

P T = T E

. Ennélfogva a feladat megoldható, ha

P T \leq T E

. Viszont egy húr szeleteinek szorzatára ismert tétel szerint

P T \cdot T E = R T \cdot T S

, így a megoldhatóság feltétele:

\begin{matrix} P T^{2} \leq R T \cdot T S . \end{matrix}

A 698. feladatban (KML XII., 3. sz. 78‐81. o.) bebizonyítottuk a háromszög szögfelezőjére vonatkozó következő egyenlőséget: a háromszög egy csúcsából húzott szögfelezőjének négyzete egyenlő a csúcsban találkozó oldalak szorzatának és a szemközti oldalon létesített szeletek szorzatának különbségével. Így a megoldhatóságra kapott feltétel a következő lesz:

\begin{matrix} P T^{2} = P R \cdot P S - R T \cdot T S \leq R T \cdot T S, \end{matrix}

átrendezve:

\begin{matrix} \frac{P R}{R T} \cdot \frac{P S}{T S} \leq 2. \end{matrix}

Mivel

P T

szögfelező, azért

\begin{matrix} \frac{P R}{R T} = \frac{P S}{T S} = \frac{P R + P S}{R S} . \end{matrix}

A kapott feltétel így írható:

\begin{matrix} {(\frac{P R + P S}{R S})}^{2} \leq 2, \end{matrix}

vagyis

\begin{matrix} P R + P S \leq R S \cdot \sqrt[]{2} . \end{matrix}

Eszerint olyan

P

pontok esetén van megoldása a feladatnak, melyek távolságainak összege

R

-től és

S

-től nem nagyobb az

R S \cdot \sqrt[]{2}

állandó értéknél. A feltételnek az

R

és

S

fókuszú,

\frac{R S}{2} \sqrt[]{2}

fél nagytengelyű,

\sqrt[]{\frac{R S^{2}}{2} - \frac{R S^{2}}{4}} = \frac{R S}{2}

fél kistengelyű ellipszis kerületi és belső pontjai tesznek eleget. Ugyanarra az eredményre jutottunk tehát, mint az I. megoldásban.

Németh József (Esztergom, Ferences g. III. o. t.)