Feladat: 835. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bergmann Gy. ,  Borsi L. ,  Endrődy T. ,  Frivaldszky S. ,  Gyene A. ,  Győry K. ,  Horváth M. ,  Kisvölcsey J. ,  Kolonits F. ,  Kristóf L. ,  Mályusz K. ,  Megyesi L. ,  Meskó A. ,  Molnár J. ,  Montvay I. ,  Németh J. ,  Pásztor Erzsébet ,  Pödör B. ,  Rockenbauer A. ,  Sárközy A. ,  Schipp F. ,  Schultz Gy. ,  Stáhl J. ,  Szász D. ,  Szatmáry Z. ,  Tápai A. ,  Tatai P. ,  Várallyay L. ,  Wollner R. 
Füzet: 1958/február, 49 - 51. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):Feladatok: 1957/május: 835. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vegyük először azt a speciális esetet, mikor a megszerkesztendő k körnek három adott pontja, A, B, C egyenlő szárú háromszöget alkotnak: AB=BC (1. 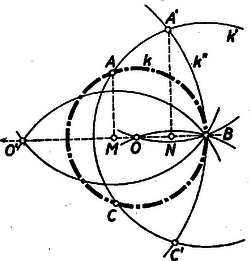ábra).

 
 
1. ábra
 

Rajzoljunk B-ből mint középpontból AB(=BC) sugárral egy k' kört, majd ugyanakkora sugárral az A és C pontok körül is. Az utóbbi két kör egymást B-n kívül még egy O' pontban is metszi, ez a pont a szimmetria következtében rajta van az ABC egyenlő szárú háromszög szimmetria-tengelyén, vagyis a megszerkesztendő k kör B-ből induló átmérőjének egyenesén. Rajzoljunk O' pont körül O'B sugárral k'' kört, majd a k' és k'' A' és B' metszéspontjaiból A'B=C'B sugarú kört. Azt állítjuk, hogy ezeknek második metszéspontja: O a keresett k kör középpontja.
Legyen ugyanis A vetülete k és k'' körök közös átmérőegyenesén M, A'-é pedig N. Ekkor a derékszögű háromszög befogójának mértani közép tulajdonsága alapján AB mértani közepe a k kör 2r átmérőjének és BM-nek, tehát:
AB2=BM⋅2r=r⋅2BM=r⋅BO',(1)
hiszen BO' húrja az A középpontú, B-n és O'-n átmérő segédkörnek és a középpontból a húrra bocsátott merőleges felezi a húrt.
Hasonlóképpen A'B mértani közepe a k'' kör átmérőjének és BN-nek:
A'B2=BN⋅2BO'=BO'⋅2BN=BO'⋅BO.(2)

De A és A' a B középpontú k' körnek a pontjai, így AB=A'B, s ezért (1) és (2) összehasonlításával látható, hogy
BO=r.

Ebből, valamint abból, hogy O a k kör átmérőegyenesén van, már következik, hogy O valóban a k kör középpontja.
Az általános esetet erre a speciális esetre vezetjük vissza. Ennek érdekében a megadott A, B és C pontokhoz olyan pontot kell csak körzővel szerkesztenünk a rajtuk átmenő körön, amely az előzőek közül kettővel egyenlő szárú háromszöget alkot.
Ezt a következőképpen végezhetjük el. Az A, B, C pontokhoz megkeressük a D pontot úgy, hogy ABCD egyenlőszárú trapéz legyen (l. 2. ábra).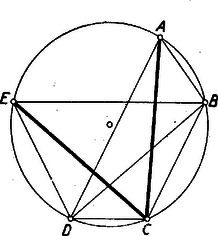
 
 
2. ábra
 

Mivel CD=AB és BD=AC, ezért a BDC háromszög szerkesztése csak körzővel igen egyszerű. (Természetesen D a trapéz egyenlő szárú volta miatt rajta lesz a keresendő körön.) Ha az ABD háromszög még nem egyenlő szárú, akkor ugyanúgy megszerkesztjük a BCDE egyenlő szárú trapéz szintén a keresett körön levő E csúcsát. A feladatot most már visszavezettük az előbb tárgyalt esetre, hiszen az ACE háromszög biztosan egyenlő szárú, AC=CE (mindkét átló a két egyenlő szárú trapéz közös BD átlójával egyezik).
Látható, hogy a szerkesztés az adott feltétel mellett (a három pont nem fekszik egy egyenesen) mindig elvégezhető s csak egy megoldásra juthatunk.
 

Megjegyzés: A megoldók nagy része körre való tükrözéssel (inverzióval) oldotta meg a feladatot. Az így kapott megoldás viszont nagyon hosszadalmas, ha az összes részletét bizonyítjuk (például az inverz pontok csak körzővel való megszerkesztését stb., amire a megoldók csak hivatkoztak). Ezért jobbnak láttuk a fentebb adott elemi megoldást közölni.