Kezdőlap


Feladat:	830. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Mályusz Károly
Füzet:	1958/január, 23 - 24. oldal		PDF \| MathML
Témakör(ök):	Csonkakúp, Terület, felszín, Térfogat, Feladat
Hivatkozás(ok):	Feladatok: 1957/április: 830. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szóban forgó csonka kúpnak és a beleállított kúpoknak egy síkmetszetét rajzoltuk meg az ábrán.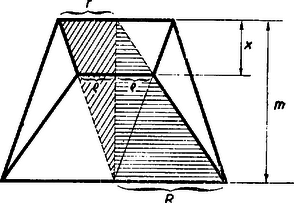

1. ábra

Az ottani jelöléseket használva a vonalazott két‐két hasonló háremszögpárból:

\begin{matrix} \frac{x}{m} = \frac{ϱ}{R} és \frac{m - x}{m} = \frac{ϱ}{r}, \end{matrix}

utóbbiból

\begin{matrix} 1 - \frac{x}{m} = \frac{ϱ}{r} . \end{matrix}

A kettőből

\begin{matrix} \frac{ϱ}{r} + \frac{ϱ}{R} = 1, ebből ϱ = \frac{R r}{R + r} . \end{matrix}

Így

\begin{matrix} x = \frac{ϱ}{R} m = \frac{r m}{R + r} \end{matrix}

és

\begin{matrix} m - x = \frac{ϱ}{r} m = \frac{R m}{R + r} . \end{matrix}

Legyen a

ϱ

és

R

, illetve

ϱ

és

r

sugarú körökkel meghatározott csonka kúpok térfogata

K_{1}

, illetve

K_{2}

. Nyilván

K_{1} + K_{2} + k = K

. A kiszámított

x

és

m - x

magasságok felhasználásával

\begin{matrix} K_{1} = \frac{m π}{3} \frac{R}{R + r} (R^{2} + R \frac{R r}{R + r} + \frac{R^{2} r^{2}}{{(R + r)}^{2}}) = \\ = \frac{m π}{3} \frac{R^{3}}{{(R + r)}^{3}} [{(R + r)}^{2}) + r (R + r) + r^{2}] = \frac{m π}{3} \frac{R^{3}}{{(R + r)}^{3}} (R^{2} + 3 R r + 3 r^{2}) . \end{matrix}

Hasonlóképpen adódik (a

R

és

τ

szerepcseréjével), hogy

\begin{matrix} K_{2} = \frac{m π}{3} \frac{r^{3}}{{(R + r)}^{3}} (3 R^{2} + 3 R r + r^{2}) . \end{matrix}

Így

\begin{matrix} K_{1} + K_{2} & = \frac{m π}{3} \frac{R^{2} (R^{3} + 3 R^{2} r + 3 R r^{2}) + r^{2} (r^{3} + 3 r^{2} R + 3 r R^{2})}{{(R + r)}^{3}} = \\ = \frac{m π}{3} \frac{R^{2} {(R + r)}^{3} + r^{2} {(R + r)}^{3} - R^{2} r^{3} - R^{3} r^{2}}{{(R + r)}^{3}} = \frac{m π}{3} (R^{2} + r^{2} - \frac{R^{2} r^{2} (R + r)}{{(R + r)}^{3}}) . \end{matrix}

Az ismeretlen

m

-et fogjuk kiszámítani az ismert adatokkal.

\begin{matrix} k = K - (K_{1} + K_{2}) = \frac{m π}{3} (R^{2} + R r + r^{2}) - (K_{1} + K_{2}) = \\ = \frac{m π}{3} (R^{2} + R r + r^{2} - R^{2} - r^{2} + \frac{R^{2} r^{2}}{{(R + r)}^{2}}) = \frac{m π}{3} \frac{R^{2} + 3 R r + r^{2}}{{(R + r)}^{2}} R r, \end{matrix}

ebből

\begin{matrix} m = \frac{3 k {(R + r)}^{2}}{π R r (R^{2} + 3 R r + r^{2})}, \end{matrix}

s így

\begin{matrix} K = \frac{m π}{3} (R^{2} + R r + r^{2}) = \frac{k {(R + r)}^{2} (R^{2} + R r + r^{2})}{R r (R^{2} + 3 R r + r^{2})} . \end{matrix}

A palást

F

felszíne

\begin{matrix} F = π (R + r) \sqrt[]{{(R - r)}^{2} + m^{2}} = \frac{k (R + r) \sqrt[]{{(R^{2} + 3 R r + r^{2})}^{2} π^{2} R^{2} r^{2} {(R - r)}^{2} + 9 k^{2} {(R + r)}^{4}}}{R r (R^{2} + 3 R r + r^{2})} . \end{matrix}

Ezzel a feladatot megoldottuk.

Mályusz Károly (Bp. II., Rákóczi g. IV. o. t.)