Kezdőlap


Feladat:	825. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Frivaldszky Sándor , Tusnády Gábor
Füzet:	1957/december, 154 - 156. oldal		PDF \| MathML
Témakör(ök):	Merőleges affinitás, Ellipszis egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1957/április: 825. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az ellipszis egy $x_{1}$ , $y_{1}$ koordinátájú pontjában (l. az 1. ábrát) húzott érintő egyenlete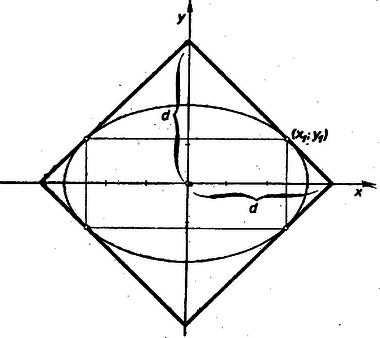

\begin{matrix} 4 x_{1} \cdot x + 9 y_{1} \cdot y = 36, \end{matrix}

azaz tengelymetszetes alakban írva

\begin{matrix} \frac{x}{\frac{9}{x_{1}}} + \frac{y}{\frac{4}{y_{1}}} = 1. \end{matrix}

1. ábra

A feladat szerint az érintő tengelymetszetei egyenlőek:

\begin{matrix} \frac{9}{x_{1}} = \frac{4}{y_{1}}, \end{matrix}

azaz

\begin{matrix} 9 y_{1} = 4 x_{1} . \end{matrix}

(1)

Felhasználhatjuk még, hogy az

(x_{1}, y_{1})

pont rajt van az, ellipszisen:

\begin{matrix} 4 x_{1}^{2} + 9 y_{1}^{2} = 36. \end{matrix}

(2)

Az (1) és (2) egyenletekből kiszámíthatjuk az

x_{1}

y_{1}

értékét:

\begin{matrix} x_{1} = \pm \frac{9 \sqrt[]{13}}{13}, y_{1} = \pm \frac{4 \sqrt[]{13}}{13} . \end{matrix}

4

, az origóra szimmetrikus érintési pontot határoz meg. Az érintési pontok által alkotott téglalap területét megkapjuk, ha pl. egy kis téglalap területét

4

-szer vesszük:

\begin{matrix} t = 4 \cdot \frac{9 \sqrt[]{13}}{13} \cdot \frac{4 \sqrt[]{13}}{13} = \frac{144}{13} = 11 \frac{1}{13} . \end{matrix}

Frivaldszky Sándor (Bp. II., Rákóczi g. IV. o. t.)

II. megoldás: Legyen a keresett négyzet átlójának hossza

2 d

. A négyzet oldalainak egyenlete rendre

\begin{matrix} y = - x + d, & y = - x - d \\ y = x + d, & y = x - d . \end{matrix}

Határozzuk meg pl. az első egyenes és az ellipszis metszéspontját. Az egyenes egyenletéből

y

értékét az ellipszis egyenletébe helyettesítve

\begin{matrix} 4 x^{2} + 9 x^{2} - 18 d x + 9 d^{2} = 36, \\ 13 x^{2} - 18 d x + 9 d^{2} - 36 = 0. & (3) \end{matrix}

Ha az egyenes érinti az ellipszist, a kapott egyenlet diszkriminánsa

0

lesz:

\begin{matrix} 324 d^{2} - 468 d^{2} + 1872 = 0. \end{matrix}

Ebből

\begin{matrix} d^{2} = 13, d = \sqrt[]{13} \end{matrix}

(mint hosszúságot, elég csak a pozitív gyököt figyelembe venni). A kapott

d

értéket (3)-ba helyettesítve, ebből az érintési pontok

x

koordinátáját kiszámíthatjuk:

\begin{matrix} x = \pm \frac{9 \sqrt[]{13}}{13} . \end{matrix}

Az első érintő egyenletéből kiszámíthatjuk az érintési pontok

y

koordinátáját

\begin{matrix} y = \pm \frac{4 \sqrt[]{13}}{13} . \end{matrix}

A területet ebből ugyanúgy számíthatjuk ki, mint az I. megoldásban.

Tusnády Gábor (Sátoraljaújhely, Kossuth g. II. o. t.)

III. megoldás: Feladatunkat koordináta geometria nélkül is megoldhatjuk. Rajzoljuk meg az ellipszissel affinitásban levő fél nagytengely sugarú kört, s húzzuk meg az

x

y

tengelyből egyaránt

d

darabot lemetsző érintőt, s ennek körrendszerbeli affin megfelelőjét (2. ábra).

2. ábra

Az affinitás viszonyszáma a fél nagytengely és fél kistengely aránya:

\frac{3}{2}

, s így a körérintő az

y

tengelyből

\frac{3}{2} d

nagyságú darabot metsz le. Az

O A B

háromszög átfogója

\frac{\sqrt[]{13}}{2} d

. Az

O A B ▵

területét kétféleképpen kiszámítva:

\begin{matrix} t = \frac{\frac{3}{2} d \cdot d}{2} = \frac{3 \cdot \frac{\sqrt[]{13}}{2} d}{2}, \end{matrix}

ebből

d = \sqrt[]{13}

.
A befogókra vonatkozó mértani közép tétellel kiszámíthatjuk a körön levő érintési pontig terjedő

A C

szakaszt:

\begin{matrix} {(\sqrt[]{13})}^{2} = A C \cdot \frac{\sqrt[]{13}}{2} \sqrt[]{13}, \end{matrix}

ebből

\begin{matrix} A C = 2. \end{matrix}

C D A

és

B O A

hasonló háromszögek felhasználásával látható, hogy az

A O = \sqrt[]{13}

távolságot a

D

pont

A C : C B = 2 : \frac{9}{2} = 4 : 9

arányban osztja, s így az

E

érintési pont

x

koordinátája

\frac{9 \sqrt[]{13}}{13}

. Ugyanúgy a

B_{1} O A

és

E D A

hasonló háromszögekben az arányszám szintén

4 : 9

, s így

O B_{1} = \sqrt[]{13}

oldal kicsinyítésével az érintési pont

y

koordinátája

E D = \frac{4 \sqrt[]{13}}{13}

.
Innen a területre ugyanaz az érték adódik, mint az előző megoldásokban.