Kezdőlap


Feladat:	820. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Győry Kálmán , Szatmáry Zoltán
Füzet:	1957/december, 148 - 149. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Ellipszis, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1957/március: 820. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Nyilvánvaló, hogy a maximális sugarú kör érinti az ellipszist, tehát meg kell határozni azt a kört, melynek középpontja a kistengely egy végpontja, és amely érinti az ellipszist. A betűzést az ábra mutatja.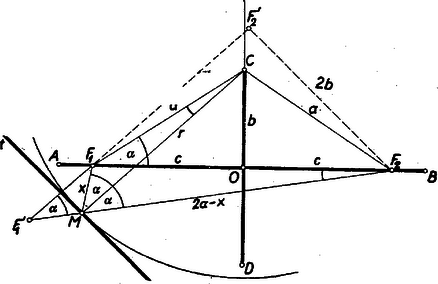

Legyen

C

a keresett kör középpontja és az egyik érintési pontja

M

. Előfordulhat (mint alább látni fogjuk), hogy ez a kistengely másik végpontja. Ezt egyelőre zárjuk ki, a kistengelyre nézve tükrös

M'

érintési pont különbözzék

M

-től. Tehát feltételeztük, hogy

r > 2 b

.
Az

M

érintési pontban a kör és ellipszis érintője, és így normálisa is közös. Tehát az

M C

körsugár merőleges a

t

közös érintőre, és az az egyenes mint az ellipszis normálisa felezi a vezérsugarak

F_{1} M F_{2} ∢ = 2 α

szögét. Tehát

F_{1} M C ∢ = C M F_{2} ∢ = α

. Legyen

F_{1}

tükörképe a

t

egyenesre nézve

F'_{1}

, akkor

F'_{1}

rajta van az

F_{2} M

vezérsugáron, és

F_{1}' F_{2} = 2 a

, továbbá az

F_{1} F'_{1} F_{2} ∢

mint megfelelő szög szintén

α

, mert

F_{1} F'_{1} ⊥ t

, és így

F_{1} F'_{1} ∥ C M

.
Mivel az

F_{1} C = C F_{2} = a

szakaszok az

M

pontból egyenlő szög alatt látszanak, azért

C F_{1} M F_{2}

négyszög húrnégyszög, és így az

\begin{matrix} F_{1} C M ∢ = F_{1} F_{2} M ∢ . \end{matrix}

Ebből következik a szögek egyenlősége miatt, hogy a

\begin{matrix} F'_{1} F_{2} F_{1 ▵} \sim M C F_{1 ▵}, \end{matrix}

vagyis

\begin{matrix} \frac{F'_{1} F_{2}}{F_{1} F_{2}} = \frac{M C}{F_{1} C}, azaz \frac{2 a}{2 c} = \frac{r}{a}, \end{matrix}

amiből

r

-re a könnyen szerkeszthető

\begin{matrix} r = \frac{a^{2}}{c} \end{matrix}

értéket kapjuk.
Húrnégyszögünkben a

C F_{1} F_{2} ∢ = C M F_{2} ∢ = α

, vagyis az

F_{1} O C

derékszögű háromszögben

b = a sin α

. Messe az

F_{2}

ből az

F'_{1} F_{1}

-re bocsátott merőleges az utóbbi egyenest

F'_{2}

-ben, akkor az

F'_{1} F'_{2} F_{2}

derékszögű háromszögben

F'_{2} F_{2} = F'_{1} F_{2} sin α = 2 a sin α = 2 b

.
Az

F'_{1} F_{1} F_{2} ▵

tehát csak akkor szerkeszthető, ha az

F_{2}

-ből rajzolt

F_{2} F_{1} = 2 c

sugarú kör metszi az

F'_{1} F_{1}

szárat, vagyis ha

2 c > 2 b

, azaz

c > b

. Ez esetben

r = \frac{a^{2}}{c} > 2 b

és

M \neq M'

.
A határesetben, ha

b = c

{(b - c)}^{2} = 0

b^{2} + c^{2} = 2 b c

, vagyis

a^{2} = 2 b c

, akkor

r = \frac{a^{2}}{c} = 2 b

. Ez esetben

M \equiv M' \equiv D

, a kistengely másik végpontja.
Ha

b > c

, akkor

r = 2 b

Szatmáry Zoltán (Bp. VIII., Piarista g. IV. o. t.)

II. megoldás: Ábránkon az

F_{1} M

vezérsugarat

x

-szel jelölve, akkor

F_{2} M = 2 a - x

, és a

C F_{1} M F_{2}

húrnégyszögre felírva Ptolemaios tételét:

\begin{matrix} r \cdot 2 c = a (2 a - x) + a x, \end{matrix}

amiből

\begin{matrix} r = \frac{2 a^{2}}{2 c} = \frac{a^{2}}{c} . \end{matrix}

Ez a megoldás akkor helyes, ha az

a

a

x

2 a - x

oldalakból ‐ ebben a sorrendben ‐ húrnégyszög szerkeszthető. Könnyen belátható, ha a húrnégyszög

C

-nél levő szöge hegyes, vagyis

b > c

, akkor a húrnégyszög

M

-ból kiinduló két oldalának összege kisebb, mint a

C

-ből kiinduló két oldal

a + a = 2 a

összege. Ez esetben tehát megfelelő húrnégyszög nem létezik. Tehát kell, hogy

b \leq c

legyen.

Győry Kálmán (Ózd, József A. g. III. o. t.)