Kezdőlap


Feladat:	819. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1957/november, 110 - 111. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Kör egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1957/március: 819. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás: Mivel $(ξ, η)$ a körön van, (l. az ábrát), kell, hogy

\begin{matrix} ξ^{2} + η^{2} = 1 \end{matrix}

(1)

teljesüljön.

P (ξ, η)

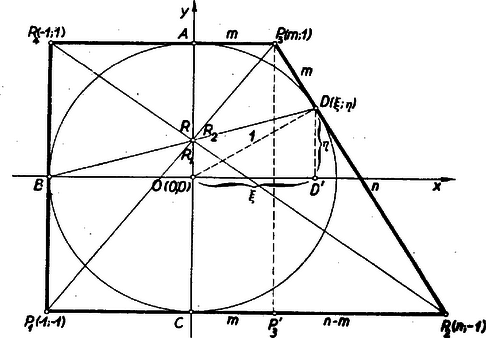pontban a körérintő az

\frac{η}{ξ}

iránytangensű

O P

egyenesre merőlegesen húzott egyenes, ennek egyenlete

\begin{matrix} y - η = - \frac{ξ}{η} (x - ξ), η y - η^{2} = - ξ x + ξ^{2}, \end{matrix}

azaz

\begin{matrix} ξ x + η y = ξ^{2} + η^{2} = 1. \end{matrix}

Ez a trapézoldal a párhuzamos trapézoldalakat

(y = - 1, y = + 1)

\begin{matrix} P_{2} (\frac{1 + η}{ξ}, - 1), P_{3} (\frac{1 - η}{ξ}, 1) \end{matrix}

pontokban metszi. Az abszcisszákat

x_{2}

és

x_{3}

-mal jelölve a

P_{1} P_{3}

átló egyenlete

\begin{matrix} y - 1 = \frac{- 2}{x_{2} + 1} (x + 1), vagyis y = - \frac{2}{x_{2} + 1} x + \frac{x_{2} - 1}{x_{2} + 1}, \end{matrix}

P_{2} P_{4}

átló egyenlete

\begin{matrix} y + 1 = \frac{2}{x_{3} + 1} (x + 1), vagyis y = \frac{2}{x_{3} + 1} x + \frac{1 - x_{3}}{1 + x_{3}} . \end{matrix}

y

-tengelyből lemetszett részek különbsége

\begin{matrix} \frac{x_{2} - 1}{x_{2} + 1} - \frac{1 - x_{3}}{1 + x_{3}} = \frac{x_{2} x_{3} + x_{2} - x_{3} - 1 + x_{2} x_{3} - x_{2} + x_{3} - 1}{(x_{2} + 1) (x_{3} + 1)} . \end{matrix}

A számlálót összevonva és

x_{2}

x_{3}

értékét beírva

\begin{matrix} 2 (x_{2} x_{3} - 1) = 2 (\frac{1 + η}{ξ} \frac{1 - η}{ξ} - 1) = \frac{1 - η^{2} - ξ^{2}}{ξ^{2}} = 0 \end{matrix}

(1) szerint, tehát a két átló az

y

-tengelyen metszi egymást.
A nem párhuzamos oldalak érintési pontjait összekötő egyenes egyenlete

\begin{matrix} y = \frac{η}{ξ + 1} (x + 1) = \frac{η}{ξ + 1} x + \frac{η}{ξ + 1} . \end{matrix}

y

-tengelyből lemetszett részt a

P_{1} P_{3}

átlónál nyert értékekből levonva és

x_{2}

értékét beírva

\begin{matrix} \frac{\frac{1 + η}{ξ} - 1}{\frac{1 + η}{ξ} + 1} - \frac{η}{1 + ξ} = \frac{1 + η - ξ}{1 + η + ξ} - \frac{η}{1 + ξ} = \frac{1 - ξ^{2} + η (1 + ξ) - η (1 + ξ) - η^{2}}{(1 + η + ξ) (1 + ξ)} = 0, \end{matrix}

tehát az érintési pontok összekötő egyenese átmegy az átlók metszéspontján.

Megjegyzés: Ha figyelembe vesszük, hogy feladatunkban az

y

-tengely a párhuzamos oldalak érintési pontjait összekötő egyenes, akkor az eredményt így fogalmazhatjuk: a szemközti oldalak érintési pontjait összekötő egyenesek és az átlók egy ponton mennek keresztül. Ilyen formában az állítás minden érintőnégyszögre igaz.