Kezdőlap


Feladat:	818. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ortutay Miklós
Füzet:	1957/november, 109 - 110. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Húrnégyszögek, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1957/március: 818. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Minden négyszög területe (akár konvex, akár konkáv) legalább az egyik átlóval két háromszög területének összegére bontható. Tegyük fel, hogy $A C = e$ egy ilyen átló. A betűzést az ábra mutatja.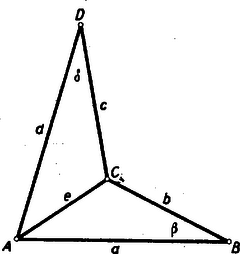

A négyszög területe

\begin{matrix} t = \frac{1}{2} a b sin β + \frac{1}{2} c d sin δ, \end{matrix}

(1)

ahol

β < 180^{\circ}

, és

δ < 180^{\circ}

.
Az

A C = e

átló négyzetét mindkét háromszögből a cosinus-tétellel kifejezve

\begin{matrix} a^{2} + b^{2} - 2 a b cos β = c^{2} + d^{2} - 2 c d cos δ, \end{matrix}

vagyis

\begin{matrix} a^{2} + b^{2} - c^{2} - d^{2} = 2 a b cos β - 2 c d cos δ . \end{matrix}

(2)

(1) négyszeresének négyzetéhez hozzáadva a (2) négyzetét:

\begin{matrix} 16 t^{2} + {(a^{2} + b^{2} - c^{2} - d^{2})}^{2} = {(2 a b sin β + 2 c d sin δ)}^{2} + {(2 a b cos β - 2 c d cos δ)}^{2} \end{matrix}

A jobb oldalt tagokra bontva és figyelembe véve, hogy

sin^{2} β + cos^{2} β = sin^{2} δ + cos^{2} δ = 1

\begin{matrix} 16 t^{2} + {(a^{2} + b^{2} - c^{2} - d^{2})}^{2} = 4 a^{2} b^{2} + 4 c^{2} d^{2} - 8 a b c d (cos β cos δ - sin β sin δ), \end{matrix}

vagyis

\begin{matrix} 16 t^{2} = 4 a^{2} b^{2} + 4 c^{2} d^{2} - {(a^{2} + b^{2} - c^{2} - d^{2})}^{2} - 8 a b c d cos (β + δ) . \end{matrix}

16 t^{2}

érték ‐ adott

a

b

c

d

oldalak esetén ‐ tehát csak a

c o s (β + δ)

értékétől függ, mégpedig

16 t^{2}

-nek, és vele a pozitív

t

-nek akkor van maximuma, ha a

8 a b c d cos (β + δ)

minimális, vagyis,

cos (β + δ)

értéke minimális, azaz

\begin{matrix} cos (β + δ) = - 1, ahonnan β + δ = 180^{\circ}, \end{matrix}

azaz a négyszög húrnégyszög.

Ortutay Miklós (Hajdúnánás, Körösi Csoma g. I. o. t.)