1) Legyen $n$ $r$-nek osztója, akkor $r\alpha =\frac{r}{n}2\pi$, és mivel $\frac{r}{n}$ a feltétel szerint egész szám az a) összeg minden tagja $0$, tehát az összeg is $0$. Az $n$-tagú b) összeg minden tagja pedig $1$, és így az összeg értéke $n$.
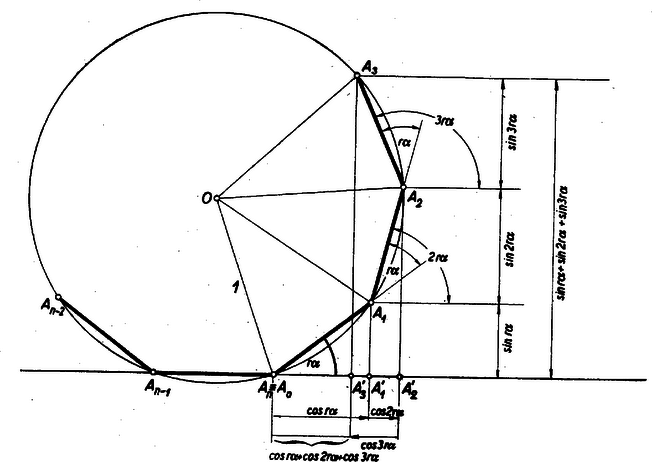
2. Ha $n$ nem osztója $r$-nek, akkor mérjük fel egy $O$ középpontú egységsugarú körben egymás után egy $A_0$ pontból kiindulva az $r\alpha$ középponti szöget. Akkor a körön az $A_1\left(r\alpha \right)$, $A_2\left(2r\alpha \right)$, $A_3\left(3r\alpha \right)$, $\text{...}$, $A_n\left(nr\alpha \right)$ szögpontokhoz jutunk. Mivel $nr\alpha =n\frac{r\cdot 2\pi }{n}=r\cdot 2\pi$, azért az $n$-edik méréssel mindenesetre (esetleg több körüljárás után és esetleg már korábban is) visszaérkezünk a kiindulási $A_0$ ponthoz, vagyis a szögpontok egy szabályos sokszög, illetőleg csillagsokszög csúcspontjai.