| Feladat: | 810. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Elbert Árpád , Kolonits Ferenc , Tatai Péter | ||
| Füzet: | 1957/november, 99 - 101. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Háromszögek hasonlósága, Pont körüli forgatás, Magasságvonal, Háromszög nevezetes vonalai, A háromszögek nevezetes pontjai, Egyenesek egyenlete, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1957/február: 810. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: A megoldók túlnyomórésze koordináta-geometriát használt. A derékszögű koordináta-rendszerben ábránkat sokféleképpen helyezhetjük el. 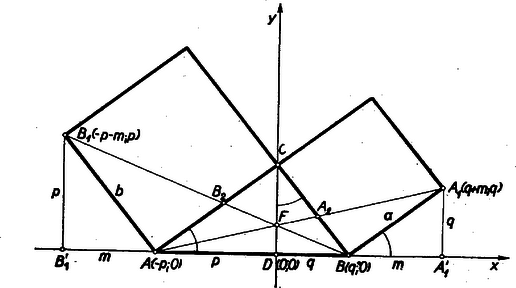 Az egyenes egyenlete:
(1) és (2) egybevetéséből Ezzel igazoltuk a feladat állítását. II. megoldás: Legyenek az és egyenesek metszéspontjai a szemközti befogón , illetőleg (1. ábra). A Ceva-féle tétel felhasználásával bizonyítjuk, hogy az , és egyenesek egy ponton mennek át. Az egyes oldalakon keletkező osztóviszonyok:
III. megoldás: Koordináta-geometria és a Ceva-féle tétel nélkül is célhoz juthatunk. Az 1. ábra betűzését megtartva, tegyük fel, hogy az egyenes a magasságot egy , a egyenes pedig a magasságot egy pontban metszi. Mivel
Tehát (1) és (2) egybevetéséből következik, hogy
IV. megoldás: Egészítsük ki az ábrát az négyzetté (2. ábra). 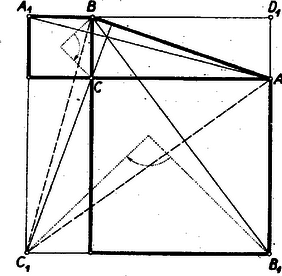 Hasonlóan látható azonban az is, ha a nagy négyzetet forgatjuk el -kal a középpontja körül úgy, hogy a -be kerüljön, hogy az -re és a -re merőleges, mert a mondott elforgatásnál a háromszög a háromszögre kerül. Arra jutottunk, hogy , és magasságvonalai az -nek, tehát igaz a feladat állítása, hogy egy ponton mennek keresztül.
|