Kezdőlap


Feladat:	806. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Jajczay Ágnes
Füzet:	1957/október, 52 - 53. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenlőtlenségek, Kör egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1957/február: 806. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A másodfokú egyenlet gyökei valósak, ha a diszkrimináns nem negatív, vagyis ha

\begin{matrix} {(m - 1)}^{2} - 4 (m + 2) = m^{2} - 6 m - 7 = (m - 7) (m + 1) \geq 0. \end{matrix}

Ez nyilván akkor teljesül, ha mindkét tényező egyidejűleg egyenlő előjelű. Mindkét gyök pozitív, ha az

m > 7

, és mindkét gyök negatív, ha

m < - 1

- 1 < m < 7

esetén egyenletünknek nincsen valós gyöke.
a) A két kör kívülről érintkezik, ha az egyik gyök pozitív, a másik negatív. Ez esetben a gyökök szorzata negatív, vagyis az állandó tag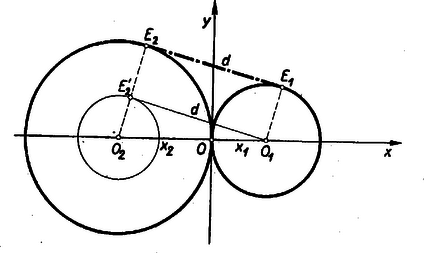

\begin{matrix} m + 2 < 0, azaz m < - 2. \end{matrix}

(Az

m = - 2

határesetben az egyik kör ponttá zsugorodik.)
b) A két kör sugara egyenlő, ha

\begin{matrix} x_{1} = - x_{2}, \end{matrix}

vagyis

\begin{matrix} x_{1} + x_{2} = m - 1 = 0, azaz m = 1, \end{matrix}

de akkor ‐ mint láttuk ‐ nincs valós gyök.
Tehát a két kör sugara nem lehet egyenlő.
c) Közös érintőszakaszról természetesen csak akkor beszélhetünk, ha a két kör kívülről érintkezik, vagyis

m < - 2

.
Az

O_{1} E'_{2} O_{2}

derékszögű háromszögből (lásd az ábrát)

\begin{matrix} d^{2} = {(x_{1} + | x_{2} |)}^{2} - {(| x_{2} | - x_{1})}^{2} = 4 x_{1} | x_{2} | = 4 (- m - 2), \end{matrix}

mert

x_{1} x_{2} = m + 2

negatív.
Tehát

\begin{matrix} d = 2 \sqrt[]{- m - 2} . \end{matrix}

Jajczay Ágnes (Bp., IX. Patrona Hungariae lg. III. o. t.)