Kezdőlap


Feladat:	804. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Papp Éva
Füzet:	1957/október, 50 - 51. oldal		PDF \| MathML
Témakör(ök):	Fizikai jellegű feladatok, Térfogat, Síkgeometriai számítások trigonometriával, Folyadékok és gázok egyensúlya, Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1957/január: 804. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kocka az asztallappal párhuzamos éleken áthaladó, az asztallappal párhuzamos síkokkal $V_{1}$ , $V_{2}$ , $V_{3}$ köbtartalmú részekre bontható. (Lásd az 1. ábrát, amely az asztallapban levő élre merőleges síkmetszetet ábrázolja.)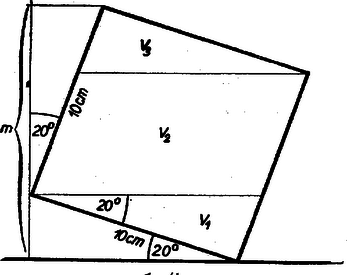

1. ábra

A szimmetria viszonyok miatt nyilvánvaló, hogy

V_{1} = V_{3}

. Jelöljük a kockában levő víz térfogatát

T

-vel. A keresett magasságot aszerint számítjuk ki, amint

\begin{matrix} T < V_{1}, & (1) \\ V_{1} < T < V_{1} + V_{2}, & (2) \\ T > V_{1} + V_{2} . & (3) \end{matrix}

A kocka köbtartalma

K = 1000 {cm}^{3}

V_{1} = V_{3} = (\frac{1}{2} 10 \cdot 10 tg 20^{\circ}) \cdot 10 = 500 tg 20^{\circ} = 182 {cm}^{3}

V_{1} + V_{2} = K - V_{3} = 818 {cm}^{3}

, és így az a), b), c) esetekben rendre (1), (2), ill. (3) szerint kell eljárni.
a)

T = 100 {cm}^{3}

, s így a víz által alkotott 3 oldalú hasáb derékszögű háromszög alakú

A P Q

alaplapjának (2. ábra) területe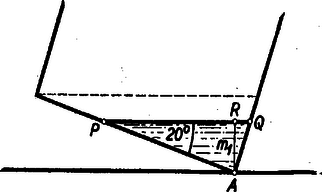

\frac{100 {cm}^{3}}{10 cm} = 10 {cm}^{2}

2. ábra

Az alaplap

P Q

átfogóját

c

-vel, a keresett

A R

magasságot

m_{1}

-gyel jelölve

\begin{matrix} c = \frac{P A}{cos 20^{\circ}} = \frac{m_{1}}{sin 20^{\circ} cos 20^{\circ}}, \end{matrix}

és így az alaplap területe

\begin{matrix} \frac{c m_{1}}{2} = \frac{m_{1}^{2}}{2 sin 20^{\circ} cos 20^{\circ}} = \frac{m_{1}^{2}}{sin 40^{\circ}} = 10, \end{matrix}

amiből

\begin{matrix} m_{1} = \sqrt[]{10 sin 40^{\circ}} = 2, 53 cm . \end{matrix}

T = 450 {cm}^{3}

, és így a víz alkotta négyoldalú egyenes hasáb

A B P_{1} Q_{1}

(3. ábra) alaplapjának területe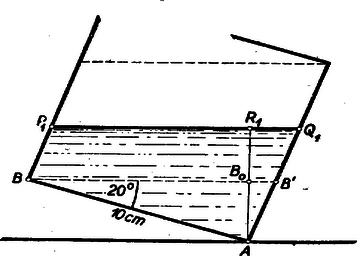

\frac{450 {cm}^{3}}{10 cm} = 45 {cm}^{2}

3. ábra

Legyen a keresett magasság

A R_{1} = A B_{0} + B_{0} R_{1} = m_{2}

\begin{matrix} A B_{0} = 10 sin 20^{\circ} = 3, 42 cm . \end{matrix}

A B B'_{▵}

területe pedig ‐ mint láttuk ‐

\frac{182 {cm}^{3}}{10 cm} = 18, 2 {cm}^{2}

, és így a

B B' Q_{1} P_{1}

paralelogramma területe

45 - 18, 2 = 26, 8 {cm}^{2}

. Tehát

\begin{matrix} B B' \cdot B_{0} R_{1} = \frac{10}{cos 20^{\circ}} \cdot B_{0} R_{1} = 26, 8. \end{matrix}

Ebből

\begin{matrix} B_{0} R_{1} = 2, 68 cos 20^{\circ} = 2, 52 cm, \end{matrix}

tehát a keresett magasság

\begin{matrix} m_{2} = 3, 42 + 2, 52 = 5, 94 cm . \end{matrix}

c) Ez esetben a kocka vízmentes része ‐ a centrális szimmetria folytán ‐ egybevágó azzal a hasábbal, melyet az a) esetben a víz alkot, tehát a keresett magasság

m_{3} = m - m_{1}

, ahol

m

jelenti az asztallaptól legtávolabbi kockaél távolságát az asztallaptól, vagyis (1. ábra)

\begin{matrix} m = 10 sin 20^{\circ} + 10 cos 20^{\circ} = 10 (sin 20^{\circ} + cos 20^{\circ}) = 12, 82 cm, \end{matrix}

és így

\begin{matrix} m_{3} = m - m_{1} = 12, 82 - 2, 53 = 10, 29 cm . \end{matrix}

Papp Éva (Bp. VIII., Ságvári E. lg. II. o. t.)