Kezdőlap


Feladat:	780. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Argay Gyula , Bácsy E. , Borsi L. , Brickner L. , Csapódy M. , Frivaldszky S. , Gáti Gy. , Gereben Ildikó , Győry Kálmán , Kozma T. , Rockenbauer A. , Schipp F. , Solt Gy. , Soós T. , Stáhl J. , Szatmáry Z. , Tatai P.
Füzet:	1957/március, 75 - 77. oldal		PDF \| MathML
Témakör(ök):	Négyszögek geometriája, Tetraéderek, Geometriai valószínűség, Feladat
Hivatkozás(ok):	Feladatok: 1956/október: 780. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Négyszög létezésének szükséges és elégséges feltétele, hogy bármely oldala kisebb legyen a másik három oldal összegénél. Jelöljük a négyszög oldalait $x$ , $y$ , $z$ , $u$ -val, és legyen a kerülete $x + y + z + u = 2 s$ . A fentiek szerint

\begin{matrix} x < y + z + u . \end{matrix}

Mindkét oldalhoz

x

-et adva, és

2

-vel osztva nyerjük, hogy

\begin{matrix} x < s . \end{matrix}

Teljesen hasonlóan adódnak az

\begin{matrix} y < s, z < s, u < s \end{matrix}

egyenlőtlenségek. Mivel az itt végzett átalakítások visszafelé is elvégezhetők, azért e négy egyenlőtlenség kifejezi a négyszög létezésének szükséges és elégséges feltételét.
Feladatunk tehát így is fogalmazható: Mi annak valószínűsége, hogy egy egységnyi szakaszt találomra

x

y

z

u

részekre osztva

\begin{matrix} x < \frac{1}{2}, y < \frac{1}{2}, z < \frac{1}{2}, u < \frac{1}{2} . \end{matrix}

Ábrázoljuk a derékszögű koordináta-rendszerben az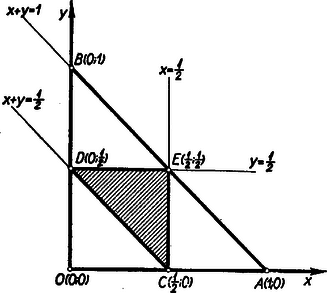

\begin{matrix} x + y = 1 - (z + u) \end{matrix}

függvényt, hol

z

-t és

u

-t egyelőre állandónak tekintjük. Ez nyilván egy egyenes, amely mind az

x

, mind az

y

tengelyből

1 - (z + u)

hosszúságú szakaszt vág le. Mivel

1 - (z + u)

maximuma

1

, és minimuma

0

, azért az összes lehetséges eseteket az

O (0; 0)

A (1; 0)

B (0; 1)

pontok által (ld. az ábrát) meghatározott háromszög belsejében levő pontok jellemzik.

Az előbbiek értelmében kedvezők csak az olyan

(x; y)

pontok, amelyekre nézve

\begin{matrix} x < \frac{1}{2}, y < \frac{1}{2} . \end{matrix}

(1)

Most két egyenlő esélyes, vagylagos esetet kell megkülönböztetni:

\begin{matrix} x + y \geq \frac{1}{2}, vagy & (a) \\ x + y < \frac{1}{2} . & (b) \end{matrix}

(a) Az

x + y > \frac{1}{2}

egyenlőtlenségnek eleget tevő pontok az

\begin{matrix} x + y = \frac{1}{2} \end{matrix}

egyenesnek ellenkező oldalán vannak, mint az origo.
Tehát a

C (\frac{1}{2}; 0)

D (0; \frac{1}{2})

és

E (\frac{1}{2}; \frac{1}{2})

pontok által meghatározott háromszög belsejében fekvő pontok koordinátái (és csakis ezek) elégítik ki mind az (1), mind az (a) követelményt. De ha (a) teljesül, akkor

\begin{matrix} z + u \leq \frac{1}{2}, \end{matrix}

és így

z < \frac{1}{2}

, és

u < \frac{1}{2}

is teljesül.
Tehát az (a) esetben a

C D E △

területe törve az

A O B △

területével adja meg a négyszög létezésének valószínűségét, vagyis

\begin{matrix} v_{a} = \frac{\frac{1}{8}}{\frac{1}{2}} = \frac{1}{4} . \end{matrix}

A (b) esetben

z + u > \frac{1}{2}

, és most az előbbi meggondolásokat egy

z

és

u

tengelyű derékszögű koordináta-rendszerben végezve el a

(z; u)

pontokra, ugyanígy kapjuk, hogy

\begin{matrix} v_{b} = \frac{1}{4} . \end{matrix}

Tehát a keresett valószínűség

\begin{matrix} v = v_{a} + v_{b} = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} . \end{matrix}

Győry Kálmán (Ózd, József Attila g. III. o. t.)

II. megoldás: Egyszerű és elegáns megoldáshoz jutunk, ha felhasználjuk a következő segédtételt: A szabályos tetraéder egy belső pontjának a négy oldallaptól való távolságainak összege a tetraéder magasságával egyenlő.
Legyen ugyanis a tetraéder magassága

m

, egy oldallap területe

t

, a

P

pont távolsága az oldallapoktól rendre

m_{1}

m_{2}

m_{3}

és

m_{4}

. A

P

pont mindegyik oldallappal egy háromoldalú gúlát határoz meg. E

4

részgúla köbtartalmainak összege egyenlő az eredeti tetraéder köbtartalmával. Tehát

\begin{matrix} \frac{t m_{1}}{3} + \frac{t m_{2}}{3} + \frac{t m_{3}}{3} + \frac{t m_{4}}{3} = \frac{t m}{3} \end{matrix}

ahonnan

\begin{matrix} m_{1} + m_{2} + m_{3} + m_{4} = m . \end{matrix}

Legyen az adott szakasz

m

, és tekintsünk egy

m

magasságú szabályos tetraédert. E tetraéder minden belső pontjának az oldallapoktól mért

m_{1}

m_{2}

m_{3}

m_{4}

távolságai ‐ a segédtétel szerint ‐

m

-nek egy lehetséges felbontását jellemzik. Kedvezőek, csak azok a pontok (amint azt a I. megoldásban láttuk), amelyekre nézve

m_{i} < \frac{m}{2} (i = 1,2,3,4)

. A kedvező pontok tehát a tetraéder éleinek felezőpontjai, mint csúcsok által meghatározott oktaéder belsejében vannak. A keresett valószínűség tehát az oktaéder és a tetraéder köbtartalmának aránya.
Legyen a tetraéder köbtartalma

K

. Az oktaéder úgy keletkeztethető, hogy az eredeti tetraéderből a

4

élfelezősík által lemetszett

4

félélhosszúságú szabályos tetraédert eltávolítjuk. Utóbbiak mindegyikének köbtartalma

{(\frac{1}{2})}^{3} \cdot K = \frac{K}{8}

, és így a

4

lemetszett tetraéder köbtartalmának összege

\frac{K}{2}

. A megmaradt oktaéder köbtartalma tehát

K - \frac{K}{2} = \frac{K}{2}

, vagyis a keresett valószínűség

\begin{matrix} v = \frac{\frac{K}{2}}{K} = \frac{1}{2} . \end{matrix}

Argay Gyula (Balassagyarmat, Balassi g. IV. o. t.)