Kezdőlap


Feladat:	772. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Kristóf László , Németh József
Füzet:	1957/február, 38 - 41. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Terület, felszín, Térgeometriai bizonyítások, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1956/szeptember: 772. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen a tetraéder köbtartalma $K$ , felszíne $F$ , a beírt gömb sugara $ϱ$ , a lapokhoz tartozó testmagasságok rendre $m_{1}$ , $m_{2}$ , $m_{3}$ , $m_{4}$ , akkor (mivel a gúla síkmetszeteinek területei úgy aránylanak, mint a gúla csúcspontjától a metszősíkokig mért távolságok négyzete):

\begin{matrix} S = \frac{{(m_{1} - 2 ϱ)}^{2}}{m_{1}^{2}} + \frac{{(m_{2} - 2 ϱ)}^{2}}{m_{2}^{2}} + \frac{{(m_{3} - 2 ϱ)}^{2}}{m_{3}^{2}} + \frac{{(m_{4} - 2 ϱ)}^{2}}{m_{4}^{2}} = \\ = 4 - 4 ϱ (\frac{1}{m_{1}} + \frac{1}{m_{2}} + \frac{1}{m_{3}} + \frac{1}{m_{4}}) + 4 ϱ^{2} (\frac{1}{m_{1}^{2}} + \frac{1}{m_{2}^{2}} + \frac{1}{m_{3}^{2}} + \frac{1}{m_{4}^{2}}) . \end{matrix}

\begin{matrix} t_{i} m_{i} = 3 K = F ϱ, (i = 1,2,3,4) \end{matrix}

ahonnan

\begin{matrix} \frac{1}{m_{i}} = \frac{t_{i}}{F ϱ}, \frac{1}{m_{i}^{2}} = \frac{t_{i}^{2}}{F^{2} ϱ^{2}}, \end{matrix}

tehát

\begin{matrix} S = 4 - 4 ϱ \frac{t_{1} + t_{2} + t_{3} + t_{4}}{F ϱ} + 4 ϱ^{2} \frac{t_{1}^{2} + t_{2}^{2} + t_{3}^{2} + t_{4}^{2}}{F^{2} ϱ^{2}} = \\ = 4 - 4 \frac{F}{F} + \frac{4 (t_{1}^{2} + t_{2}^{2} + t_{3}^{2} + t_{4}^{2})}{F^{2}} = \frac{4 (t_{1}^{2} + t_{2}^{2} + t_{3}^{2} + t_{4}^{2})}{{(t_{1} + t_{2} + t_{3} + t_{4})}^{2}} . \end{matrix}

Bebizonyítjuk, hogy itt a számláló legalább akkora, mint a nevező. Mivel

\begin{matrix} {(t_{1} - t_{2})}^{2} + {(t_{1} - t_{3})}^{2} + {(t_{1} - t_{4})}^{2} + {(t_{2} - t_{3})}^{2} + {(t_{2} - t_{4})}^{2} + {(t_{3} - t_{4})}^{2} \geq 0, \end{matrix}

(1)

így

\begin{matrix} 3 (t_{1}^{2} + t_{2}^{2} + t_{3}^{2} + t_{4}^{2}) \geq 2 (t_{1} t_{2} + t_{1} t_{3} + t_{1} t_{4} + t_{2} t_{3} + t_{2} t_{4} + t_{3} t_{4}) . \end{matrix}

Mindkét oldalhoz

(t_{1}^{2} + t_{2}^{2} + t_{3}^{2} + t_{4}^{2})

-et hozzáadva

\begin{matrix} 4 (t_{1}^{2} + t_{2}^{2} + t_{3}^{2} + t_{4}^{2}) \geq {(t_{1} + t_{2} + t_{3} + t_{4})}^{2}, \end{matrix}

azaz tényleg

\begin{matrix} S = \frac{4 (t_{1}^{2} + t_{2}^{2} + t_{3}^{2} + t_{4}^{2})}{{(t_{1} + t_{2} + t_{3} + t_{4})}^{2}} \geq 1. \end{matrix}

Egyenlőség jele akkor és csakis akkor érvényes (1) szerint, ha

\begin{matrix} t_{1} = t_{2} = t_{3} = t_{4} . \end{matrix}

Ebből azonban nem következik, hogy a tetraéder szabályos, elégséges feltétel már az is, hogy a körülírt gömb és a beírt gömb középpontjai azonosak, amikor is ‐ mint ismeretes (ld. K. M. L. 592. feladat, IX. kötet 111. oldal) ‐ a tetraéder négy lapja egybevágó.

Kristóf László (Mosonmagyaróvár, Kossuth g. III. o. t.)

II. megoldás: Bebizonyítjuk a feladatnál általánosabban a következőt: legyen a

P_{1} P_{2} P_{3} P_{4}

tetraéder egy belső pontja

O

. Az

O

pontra vonatkozó tükörképe a

Q_{1} Q_{2} Q_{3} Q_{4}

tetraéder. Ez utóbbi tetraéder síkjai messék ki az előbbi tetraéderből rendre a

τ_{1}

τ_{2}

τ_{3}

τ_{4}

területű háromszögeket, amelyeket

B_{1} C_{1} D_{1}

A_{2} C_{2} D_{2}

A_{3} B_{3} D_{3}

és

A_{4} B_{4} C_{4}

-gyel jelölünk (lásd az ábrát). A

C_{2} D_{2}

B_{3} D_{3}

és

B_{4} C_{4}

egyenesek határolta

B'_{1} C'_{1} D'_{1}

háromszög a

B_{1} C_{1} D_{1}

háromszög tükörképe. A háromszög területét ugyanúgy jelölve, mint a háromszögeket:

\begin{matrix} S = \frac{τ_{1}}{t_{1}} + \frac{τ_{2}}{t_{2}} + \frac{τ_{3}}{t_{3}} + \frac{τ_{4}}{t_{4}} = \frac{B'_{1} C'_{1} D'_{1}}{t_{1}} + \frac{A_{2} C_{2} D_{2}}{t_{2}} + \frac{A_{3} B_{3} D_{3}}{t_{3}} + \frac{A_{4} B_{4} C_{4}}{t_{4}} . \end{matrix}

A levágott tetraéderek mind hasonlóak az eredetihez, azért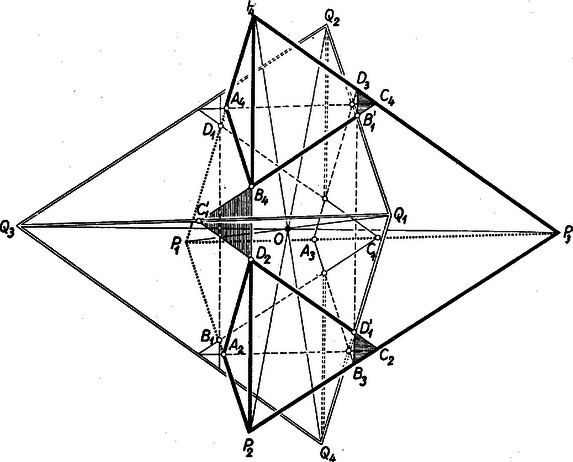

\begin{matrix} \frac{A_{2} C_{2} D_{2}}{t_{2}} = \frac{P_{2} C_{2} D_{2}}{t_{1}}, \frac{A_{3} B_{3} D_{3}}{t_{3}} = \frac{P_{3} B_{3} D_{3}}{t_{1}}, \frac{A_{4} B_{4} C_{4}}{t_{4}} = \frac{P_{4} B_{4} C_{4}}{t_{1}}, \end{matrix}

és így

\begin{matrix} S = \frac{B'_{1} C'_{1} D'_{1} + P_{2} C_{2} D_{2} + P_{3} B_{3} D_{3} + P_{4} B_{4} C_{4}}{t_{1}} . \end{matrix}

E tört számlálójában szereplő háromszögek azonban fedik a

t_{1}

-et, sőt ‐ azonfelül ‐ egyes részeket kétszeresen fedhetnek (pl. az ábrában a vízszintesen srafozott két háromszög), vagy túlnyúlhatnak (az ábrában a függőlegesen srafozott háromszög). Tehát tényleg

\begin{matrix} S \geq 1. \end{matrix}

Ha a

Q_{1}

a tetraéder belsejében van, akkor a

B'_{1} C'_{1} D'_{1}

háromszöget tartalmazza a másik három háromszög, és így még

\frac{4}{3}

-nál sem lehet kisebb az

S

összeg.

Mivel a

B'_{1} C'_{1} D'_{1} ▵

oldalai párhuzamosak a

P_{1} P_{2} P_{3} ▵

oldalaival, azért egyenlőség csak akkor állhat fenn, ha a

B_{1} C_{1} D_{1}

pontok élfelező pontok, vagyis

O

súlypont. A feladat feltételei mellett tehát

S

értéke akkor 1, ha a beírt gömb középpontja egybeesik a súlyponttal. Mivel a súlypont távolsága az egyes oldallapoktól az oldallaphoz tartozó testmagasság negyedrésze, így a beírt gömb középpontja akkor és csak akkor esik egybe a súlyponttal, ha a négy testmagasság, és így a négy oldallap területe is egyenlő. Ezzel éppen az I. megoldás feltételéhez jutottunk.

Németh József (Esztergom, Ferences g. III. o. t.)