Kezdőlap


Feladat:	771. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Rockenbauer Antal , Tatár Iván
Füzet:	1957/január, 15 - 17. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletrendszerek, Parabola egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1956/szeptember: 771. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Rendezzük át egyenleteinket a következő alakba:

\begin{matrix} y^{2} - 6 y = 8 x - x^{2}, & (1) \\ y^{2} - 6 y = - 9 x^{2}, & (2) \\ y^{2} - 6 y = λ (x + 1) - 9. & (3) \end{matrix}

Az (1), (2) egyenletrendszer összes megoldásait meghatározva vizsgáljuk meg, hogy

λ

milyen értékei mellett elégítik ki azok a (3) egyenletet.
(1) és (2) jobboldalait egyenlővé téve

\begin{matrix} 8 x^{2} + 8 x = 0, vagyis x (x + 1) = 0, \end{matrix}

ahonnan

\begin{matrix} x_{1} = 0, x_{2} = - 1. \end{matrix}

x_{1}

-et (2)-be helyettesítve

\begin{matrix} y (y - 6) = 0, \end{matrix}

amiből

\begin{matrix} y_{1,1} = 0, y_{1,2} = 6. \end{matrix}

x^{2}

behelyettesítése után

\begin{matrix} y^{2} - 6 y + 9 = 0, vagyis {(y - 3)}^{2} = 0, \end{matrix}

amiből

\begin{matrix} y_{2,1} = y_{2,2} = 3. \end{matrix}

(1) és (2) gyökei tehát (0, 0); (0,

6

); és a kétszeresen számító (

- 1

, 3).
Ezeket az értékpárokat rendre (3)-ba helyettesítve

\begin{matrix} 0 & = λ - 9, amiből λ = 9, & (3a) \\ 36 - 36 & = λ - 9, ahonnan λ = 9, & (3b) \\ 0 & = 0, amiλ-tól független azonosság . & (3c) \end{matrix}

Az első két értékpár

λ = 9

esetén elégíti ki mind a három egyenletet, míg a harmadik értékpár

λ

bármely értékénél kielégíti azokat. Minthogy az (1), (2) összes megoldásait figyelembe vettük, több megoldása nem is lehet az egyenletrendszernek.
A feladat és megoldás geometriai értelmezéséhez alakítsuk át az egyenleteket.
(1)-ben hozzunk minden tagot a baloldalra és azután adjuk mindkét oldalhoz

3^{2} + 4^{2}

-t.

\begin{matrix} x^{2} - 8 x + 16 + y^{2} - 6 y + 9 = 25, \\ {(x - 4)}^{2} + {(y - 3)}^{2} = 5^{2} . & (1') \end{matrix}

Ez kör egyenlete, melynek, sugara 5 egység, középpontjának koordinátái: (4, 3).
(2) hasonló átalakítása után kapjuk

\begin{matrix} \frac{x^{2}}{1^{2}} + \frac{{(y - 3)}^{2}}{3^{2}} = 1^{2} \end{matrix}

(

2'

)

Ez ellipszis egyenlete, melynek középpontja a (0, 3) pont, fél nagytengelye 3 egység, fél kis tengelye 1 egység, és nagytengelye a koordinátarendszer

y

tengelyén van.
(3) átalakított alakja:

\begin{matrix} {(y - 3)}^{2} = λ (x + 1) . \end{matrix}

(

3'

)

Ez parabolasereget jellemez. Közös tengelyük párhuzamos az

x

tengellyel, de 3 egységgel fel van tolva az

y

tengely mentén. Közös csúcspontjuk a (

- 1

, 3) pont. A

λ

paraméter egyrészt a parabola szárai szétágazásának mértékét befolyásolja, másrészt meghatározza azt, hogy a parabolák az

x = - 1

egyenestől jobbra (

λ > 0

), vagy balra (

λ < 0

) helyezkednek el.

λ = 0

esetben az

y = 3

egyenessé fajult parabolát kapjuk.
A feladat abból állt, hogy meghatározzuk

λ

milyen értéke mellett van a három görbének közös pontja.
Az első lépés a kör és ellipszis közös pontjainak megkeresése. Kiszámítottuk, hogy ezek a (0, 0), (0, 6) pontokban metszik, a (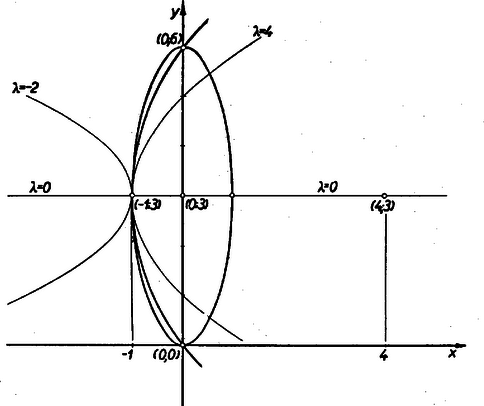

- 1

, 3) pontban pedig érintik egymást. (L. az ábrát).

A (

- 1

, 3) pont egyúttal a parabolasereg közös csúcspontja, ezért

λ

választásától függetlenül ez mindig közös pontja a három görbének.
Mivel

y = 3

magasságban a kistengellyel párhuzamosan húzott egyenes mindhárom görbének szimmetria tengelye, és a (0, 0), (0, 6) pontok erre nézve egymás tükörképei, így, ha

λ

-t úgy választjuk, hogy az egyik ponton átmenjen a parabola, akkor az már a másik metszésponton is átmegy; ez a

λ = 9

értékre következik be. (A

λ = 9

értékhez tartozó parabolát a rajzon technikai okokból nem tüntettük fel, túl közelre esik a körhöz.)
A feladat geometriai elemzése elvezet magához a megoldáshoz is, ezért ez második megoldási módnak tekinthető.

Tatár Iván (Debrecen, Ref. g. IV. o. t.)

Rockenbauer Antal (Bp. X., I. László g. IV. o. t.)