Kezdőlap


Feladat:	761. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Makkai Mihály
Füzet:	1956/december, 147. oldal		PDF \| MathML
Témakör(ök):	Hiperbola egyenlete, Hiperbola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1956/május: 761. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Helyezzük el körünket egy derékszögű koordináta-rendszerben úgy, hogy középpontja az origóban, az $A$ pont az $x$ tengely pozitív részén legyen (lásd az ábrát).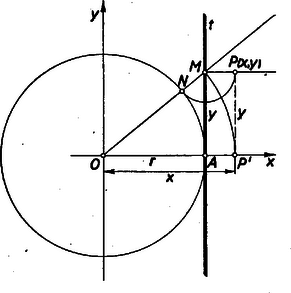

P

pont koordinátáit

x

y

-nal jelölve:

\begin{matrix} x = O A + A P' = O N + M P = O N + N M = O M, \end{matrix}

és így az

O A M

derékszögű háromszögre Pythagoras tételét alkalmazva

\begin{matrix} x^{2} = y^{2} + r^{2}, \end{matrix}

vagyis

\begin{matrix} \frac{x^{2}}{r^{2}} - \frac{y^{2}}{r^{2}} = 1. \end{matrix}

Ez egy egyenlőoldalú hiperbolának egyenlete, melynek középpontja

O

, valós féltengelye az

O A = r

szakasz.

x > r > 0

miatt csak az a hiperbolaág jön számításba, amelynek csúcspontja az adott

A

.
Megfordítva: ezen hiperbolaág bármely

P (x, y)

pontjára nézve

\begin{matrix} x^{2} = y^{2} + r^{2}, \end{matrix}

másrészt

\begin{matrix} O M^{2} = y^{2} + r^{2} . \end{matrix}

E két összefüggés egybevetéséből

\begin{matrix} x = O M, \end{matrix}

és így

\begin{matrix} x - r = O M - r, \end{matrix}

azaz

\begin{matrix} A P' = M P = M N . \end{matrix}

Tehát a

P

pont eleget tesz a feladat feltételeinek, vagyis a jelzett hiperbolaág a keresett mértani hely.

Makkai Mihály (Bp., V., Eötvös J. g. III. o. t.)