| Feladat: | 740. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Borsi L. , Frivaldszky S. , Hidas P. , Jakubovics J. , Makkai M. , Razga T. , Rockenbauer A. , Szabados J. , Szeidl B. , Vámos A. , Zentai Á. , Zsombok Zoltán | ||
| Füzet: | 1956/november, 92. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Rácsgeometria, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1956/február: 740. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Válasszuk a négyzetrács egy elemi négyzetének oldalát egységnek. Ha egy tetszőleges, önmagát nem metsző rácssokszög egy pontjából kiindulva végighaladunk a sokszög kerületén, akkor annyi rácsponton haladunk át, ahány egységnyi utat tettünk meg. A megtett egységek száma mindig páros, mert ahány egységet haladunk ,,fölfelé'', ugyanannyit kell megtennünk ,,lefelé'', és ahányat ,,jobbra'', ugyanannyit teszünk ,,balra'' is amíg a kiindulási ponthoz visszaérkezünk. Eszerint a rácssokszög kerületén fekvő rácspontok száma mindig páros, és ez a szám a rácssokszög kerületének mértékszáma. 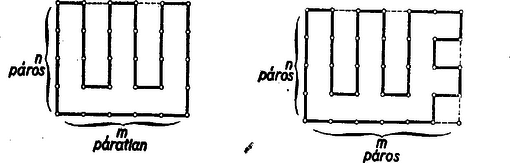 Az -es rácstéglalap összes rácspontjainak száma (a kerületén fekvő rácspontokhoz a belső rácspontokat is számítva): , tehát a benne kijelölt rácssokszög kerülete ‐ a fentiek szerint ‐ legfeljebb lehet. Két esetet kell megkülönböztetni: a) és közül legalább az egyik páratlan, b) mindkettő páros. Az a) esetben páros, és ‐ mint az 1. ábra mutatja ‐ a téglalap páratlan egységnyi oldalának ,,fésű''-szerű kiképzésével állíthatunk elő olyan rácssokszöget, amely minden rácsponton áthalad, tehát kerülete . A b) esetben páratlan, tehát a maximális kerületű rácssokszög kerülete legfeljebb lehet. Megmutatjuk, hogy ez esetben tényleg létezik egy olyan rácssokszög, amely rácspont kivételével minden rácsponton áthalad. Ugyanis hagyjunk el a rácstéglalapból pl. egy oszlopot, és a megmaradt téglalapba rajzoljunk a) szerint rácssokszöget, azután az elhagyott oszlopot a 2. ábra szerinti fogazással fűzzük hozzá. A két esetet egybefoglalva kimondhatjuk, hogy az -es rács-téglalapba írható maximális kerületű rácssokszög kerülete
|