Kezdőlap


Feladat:	739. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Argay Gyula , Danassy Károly
Füzet:	1956/november, 89 - 91. oldal		PDF \| MathML
Témakör(ök):	Negyedfokú (és arra visszavezethető) egyenletek, Menelaosz-tétel, Szinusztétel alkalmazása, Szögfüggvények, síkgeometriai számítások, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1956/február: 739. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az $A B D$ egyenlőszárú háromszögben az $A$ csúcsnál levő szög $120^{\circ}$ (lásd az ábrát), és így az 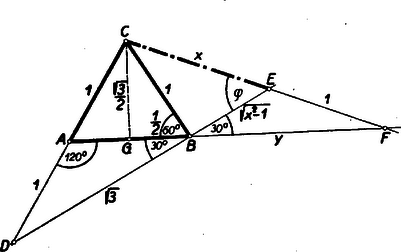$A B D ∢ = E B F ∢ = 30^{\circ}$ és a $C B E ∢ = 90^{\circ}$ .

C B E

derékszögű háromszögben a

C E B ∢

-et

φ

-vel jelölve,

\begin{matrix} x = \frac{1}{sin φ} . \end{matrix}

(1)

B E F

háromszögben a sinus-tétel szerint

\begin{matrix} 1 : y = sin 30^{\circ} : sin (180 - φ) = \frac{1}{2} : sin φ, \end{matrix}

ahonnan

\begin{matrix} y = 2 sin φ . \end{matrix}

(2)

(1) és (2) szorzata

\begin{matrix} x y = 2. \end{matrix}

(3)

A B C ▵

-ben a

C

-ből kiinduló magasság

C G = \frac{\sqrt[]{3}}{2}

. A

C G F

derékszögű háromszögre Pythagoras tételét alkalmazva:

\begin{matrix} {(\frac{\sqrt[]{3}}{2})}^{2} + {(y + \frac{1}{2})}^{2} = {(x + 1)}^{2} . \end{matrix}

A zárójeleket felbontva, összevonva,

x^{2}

-tel szorozva ‐

x^{2}

(3) miatt nem lehet

0

‐ alkalmazva (3)-at és

0

-ra redukálva

\begin{matrix} y^{4} + y^{3} - 4 y - 4 = 0. \end{matrix}

(4)

A baloldalon az első két tagból is, a második kettőből is kiemelhető

(y + 1)

\begin{matrix} (y + 1) (y^{3} - 4) = 0. \end{matrix}

Ezen egyenletnek egyetlen pozitív gyöke

\begin{matrix} y = \sqrt[^{3}]{4}, és így (3) alapján x = \frac{2}{\sqrt[^{3}]{4}} = \sqrt[^{3}]{\frac{8}{4}} = \sqrt[^{3}]{2} . \end{matrix}

Danassy Károly (Mosonmagyaróvár, Kossuth g. II. o. t.)

II. megoldás: A

C B D

derékszögű háromszögben

B D = \sqrt[]{D C^{2} - C B^{2}} = \sqrt[]{4 - 1} = \sqrt[]{3}

, a

C B E

derékszögű háromszögből pedig

B E = \sqrt[]{x^{2} - 1}

.
A

C A F ▵

-re és

D E

egyenesre felírva a Menelaos-féle tételt

\begin{matrix} (C A D) (A F B) (F C E) = (- 2) \cdot \frac{1}{y} \cdot \frac{1}{x} = - 1, \end{matrix}

vagyis

\begin{matrix} x y = 2. \end{matrix}

(5)

Ugyanígy a

C D E ▵

-re és az

A F

egyenesre vonatkozóan Menelaos tétele szerint

\begin{matrix} (C D A) (D E B) (E C F) = 1 \cdot \frac{\sqrt[]{3}}{\sqrt[]{x^{2} - 1}} \cdot (- \frac{1}{x + 1}) = - 1, \end{matrix}

vagyis

\begin{matrix} (x + 1) \sqrt[]{x^{2} - 1} = \sqrt[]{3} . \end{matrix}

Négyzetre emélés és rendezés után

\begin{matrix} x^{4} + 2 x^{3} - 2 x - 4 = 0, \end{matrix}

ami tényezőkre bontva

\begin{matrix} (x + 2) (x^{3} - 2) = 0. \end{matrix}

Ennek az egyenletnek egyetlen pozitív gyöke

\begin{matrix} x = \sqrt[^{3}]{2} és így (5) alapján y = \frac{2}{\sqrt[^{3}]{2}} = \sqrt[^{3}]{\frac{8}{2}} = \sqrt[^{3}]{4} \end{matrix}

Argay Gyula (Balassagyarmat, Balassa g. II. o. t.)

Megjegyzés: Ismeretes a deloszi probléma, amely egy olyan kocka élének megszerkesztését kívánja, amelynek köbtartalma kétszerese egy adott kocka köbtartalmának. Az adott kocka élét egységnek tekintve az

x^{3} = 2 \cdot 1^{3} = 2

egyenletből

x = \sqrt[^{3}]{2}

, amely érték tudvalevőleg körzővel és vonalzóval meg nem szerkeszthető. A jelen feladat alapján módot találunk a

\sqrt[^{3}]{2}

távolság megszerkesztésére, abban az esetben, ha szerkesztési eszközként a közönséges egyélű vonalzó helyett megengedjük az ún. ,,távolsághordó-vonalzót'', vagyis egy olyan vonalzót, amelyen az egységnyi szakasz fel van tüntetve.
A szerkesztés menete (ábránkat felhasználva): Egy

B

csúcsú

120^{\circ}

-os szög egyik szárára felmérjük

B

-től a

B C = 1

szakaszt.

B

-n át húzunk

C B

-re merőleges egyenest, amely tehát a

120^{\circ}

-os szög másik szárával

30^{\circ}

-ot zár be. A távolsághordó vonalzónkat úgy helyezzük el (

C

körül forgatva és csúsztatva ‐ papírcsíkkal mindenki megpróbálhatja), hogy

C

-hez illeszkedjék, és ugyanakkor egy egységnyi szakasz két végpontja

E

és

F

30^{\circ}

-os szög száraira kerüljön. Ebben a helyzetben ‐ mint bebizonyítottuk ‐

C E = x = \sqrt[^{3}]{2}

. (Ez is szerkesztés, de nem euklideszi.)