Kezdőlap


Feladat:	731. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ádám A. , Argay Gy. , Bánhidy Kálmán , Bartha Gyöngyi , Beke Gy. , Benkő B. , Berár I. , Császár I. , Daróczy Z. , Endrődy T. , Frivaldszky S. , Gelencsér L. , Grell M. , Harza T. , Jakubovics J. , Kengyel Vilma , Kismarty L. , Makkai M. , Razga T. , Rockenbauer A. , Schipp F. , Stáhl J. , Szabados J. , Szokoly P. , Zsombok Z.
Füzet:	1956/november, 81 - 82. oldal		PDF \| MathML
Témakör(ök):	Menelaosz-tétel, Feladat
Hivatkozás(ok):	Feladatok: 1956/január: 731. matematika feladat

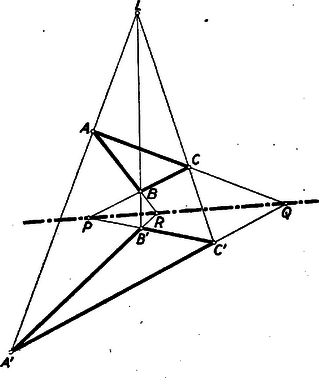
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a $B C$ és $B' C'$ metszéspontja $P$ , a $C A$ és $C' A'$ metszéspontja $Q$ , és az $A B$ és $A' B'$ metszéspontja $R$ (lásd az ábrát).

Írjuk fel a Menelaos-féle tételt az

A B L

háromszögre, és az

A' B'

egyenesre:

\begin{matrix} (A B R) (B L B') (L A A') = - 1. \end{matrix}

(1)

Hasonlóképpen nyerjük a

B C L

háromszögre és

B' C'

-re, ill. a

C A L

háromszögre és

C' A'

-re, hogy

\begin{matrix} (B C P) (C L C') (L B B') = - 1, \end{matrix}

(2)

és

\begin{matrix} (C A Q) (A L A') (L C C') = - 1. \end{matrix}

(3)

Mivel

\begin{matrix} (B L B') (L B B') = \frac{B B'}{B' L} \cdot \frac{L B'}{B' B} = 1, \end{matrix}

és hasonlóképpen

\begin{matrix} (L A A') (A L A') = 1, (C L C') (L C C') = 1, \end{matrix}

azért (1), (2) és (3) szorzata

\begin{matrix} (A B R) (A C P) (C A Q) = - 1, \end{matrix}

ami ‐ az

A B C

háromszögre a Menelaos tételének megfordítását alkalmazva ‐ éppen azt fejezi ki, hogy a

P

Q

R

pontok egy egyenesen vannak.
Fordítva, ha az

A B C

és

A' B' C'

háromszögek megfelelő oldalainak metszéspontjai, a

P

Q

R

pontok egy egyenesen vannak, akkor az

A A' R

és

C C' P

háromszögek olyanok, hogy a megfelelő csúcspontok összekötései:

A C

A' C'

és

R P

egy ponton, a

Q

ponton mennek át, de akkor a most bebizonyított tétel alapján az előbbi két háromszög megfelelő oldalainak metszéspontjai:

L

B'

B

egy egyenesen vannak, vagyis a

B B'

egyenes átmegy az

A A'

és

C C'

egyenesek

L

metszéspontján. Tehát az

A B C

és

A' B' C'

háromszögekre nézve a megfelelő pontok összekötései egy ponton, a

L

ponton mennek át.

Bánhidy Kálmán (Debrecen, Ref. gimn. IV. o. t.)

Megjegyzés: Ezzel tételünknek, amely Desargues tételeként ismeretes (lásd Obláth Richárd cikkét Vályi Gyuláról lapunk 1956 januári számában a 3. oldalon), egy síkbeli bizonyítását adtuk. Az említett cikkben a tétel térbeli bizonyítása található. (Ennek megemlítését természetesen nem fogadtuk el jelen feladat megoldásának.)