Kezdőlap


Feladat:	730. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Harza Tibor
Füzet:	1956/november, 80 - 81. oldal		PDF \| MathML
Témakör(ök):	Téglatest, Egyenes, Kör (és részhalmaza), mint mértani hely, Tetraéderek, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1956/január: 730. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egészítsük ki az $M A B N$ tetraédert hasábbá, mint az az ábrán látható.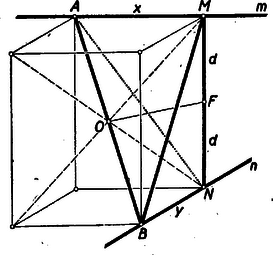

Mivel a feltételek szerint

M N ⊥ M A

M N ⊥ N B

és

M A ⊥ N B

, azért a hasáb téglatest, köréje gömb írható, amely megegyezik az

M A B N

tetraéder köré írt gömbbel, hiszen négy különböző pont, amelyek nincsenek egy síkban, egy és csakis egy gömböt határoznak meg. A keresett gömb középpontja tehát a téglatest testátlóinak közös felezőpontja. Az egyik átló

A B

. Pythagoras tételének kétszeres felhasználásával

\begin{matrix} A B = \sqrt[]{x^{2} + {(2 d)}^{2} + y^{2}} = \sqrt[]{x^{2} + y^{2} + 4 d^{2}} . \end{matrix}

A keresett gömb középpontja tehát az

A B

szakasz

O

felezőpontja és sugara

\begin{matrix} O A = O M = O N = O B = \frac{A B}{2} = \frac{1}{2} \sqrt[]{x^{2} + y^{2} + 4 d^{2}} . \end{matrix}

Mivel

O M = O N

, azért az

O

pont benne van az

M N

szakaszt merőlegesen felező síkban, amely a

M N

szakaszt az

F

felezőpontjában metszi.
a) Ha a gömb sugara állandóan

2 d

, vagyis

\begin{matrix} A O = O M = 2 d, \end{matrix}

akkor az

O F M

derékszögű háromszögben

\begin{matrix} O F = \sqrt[]{O M^{2} + M F^{2}} = \sqrt[]{4 d - d^{2}} = d \sqrt[]{3}, \end{matrix}

vagyis az

O

pontok rajta vannak egy olyan körön, amelynek síkja merőlegesen felezi a

M N

szakaszt, középpontja az

F

pont, és sugara

d \sqrt[]{3}

, s mivel megfordítva e kör minden pontja lehet egy megfelelő gömb középpontja, azért a fenti kör az

O

pontok mértani helye.
b) Ha

x = y

, akkor az

O

pontok távolsága az

[A M N]

síktól

(\frac{y}{2})

ugyanakkora, mint a

[B M N]

síktól

(\frac{x}{2})

, vagyis az

O

pontok benne vannak e két sík szögfelező síkjaiban. Az előbbiek alapján tehát az

O

pontok rajta vannak a

M N

szakaszt merőlegesen felező sík és e két szögfelező sík metszésvonalán. Ez a két metszésvonal egyúttal az

O

pontok mértani helye, mert ezen egyenesek bármely pontja lehet

O

pont.

Megjegyzés: Mindkét mértani hely könnyen általánosítható arra az esetre, a) mikor a gömb sugara

r = állandó (> d)

és b), amikor

x = k y

, ahol

k

állandó.

Harza Tibor (Székesfehérvár, József A. g. IV. o. t.)