Kezdőlap


Feladat:	724. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csiszár Imre , Daróczy Zoltán
Füzet:	1956/október, 43 - 44. oldal		PDF \| MathML
Témakör(ök):	Konstruktív megoldási módszer, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1955/december: 724. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen $D$ merőleges vetülete: $D'$ a háromszög síkjában a $P$ -től különböző pont. Akkor a $P D$ félegyenes a $P D'$ félegyenessel hegyesszöget zár be. Először megmutatjuk, hogy két $P$ -ből kiinduló síkbeli félegyenes közül az zár be nagyobb szöget a térbeli $P D$ -vel, amelyik $P D'$ -vel nagyobb szöget zár be. Vegyünk fel két $P$ -ből kiinduló tetszőleges félegyenesen egy $Q$ , illetőleg $Q_{1}$ pontot úgy, hogy 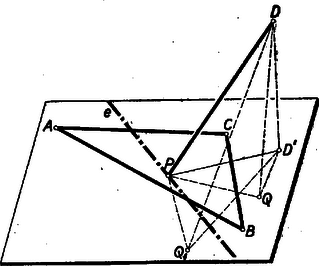$P Q = P Q_{1} = P D'$ .

1. ábra

Q P D' ∢ < Q_{1} P D' ∢

(1. ábra), akkor

D' Q < D' Q_{1}

, és így a

Q D D'

és

Q_{1} D D'

derékszögű háromszögekből

Q D < Q_{1} D

, következőleg a

Q D P

és

Q_{1} D P

háromszögekből

\begin{matrix} Q P D ∢ < Q_{1} P D ∢ . \end{matrix}

P

ponton átmenő,

D P

-re merőleges, sík a háromszög síkjából kimetsz egy

D P

-re merőleges

e

egyenest. Minden

Q

pontra nézve, mely az

e

egyenesen van a

Q P D ∢ = 90^{\circ}

, tehát az előbbiek alapján minden olyan síkban fekvő

Q

pontra, amely az

e

-nek ugyanarra az oldalára esik, mint

D'

\begin{matrix} Q P D ∢ < 90^{\circ}, \end{matrix}

e

másik oldalára eső

Q

pontokra

\begin{matrix} Q P D ∢ > 90^{\circ} . \end{matrix}

Mivel

P

a háromszögnek egyik belső pontja, azért az

e

egyenes a háromszögnek legalább egy csúcsát (az 1. ábrában az

A

-t) elválasztja

D'

-től és egyszer-smind legalább egy másik csúcstól.

Megjegyzés: Ha

P \equiv D'

, akkor mind a három szög derékszög, tehát akkor feladatunk értelmét veszti.

Daróczy Zoltán (Debrecen, Ref. g. IV. o. t.)

II. megoldás: Tekintsük az

A D

B D

és

C D

átmérőjű

G_{1}

G_{2}

G_{3}

gömböket. Thales tétele értelmében az

A P D ∢

tompa-, derék-, illetve hegyesszög, aszerint, amint

P

G_{1}

-n belül, a

G_{1}

-en rajta, ill. a

G_{1}

-en kívül van. Hasonló megállapítások érvényesek a másik két szögre és a másik két gömbre vonatkozólag. Háromszögünk síkja a három gömbből kimetszi rendre a

k_{1}

k_{2}

k_{3}

köröket (2. ábra), melyeknek átmérőjük a gömbátmérőknek vetületei: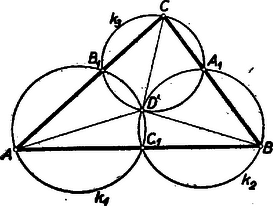

A D'

B D'

C D'

2. ábra

A három kör mindegyike tehát átmegy a

D'

ponton, és 2‐2 kör második metszéspontja (

A_{1}

B_{1}

C_{1}

) a Thales tétele alapján rajta van egy-egy háromszögoldalon (vagy annak meghosszabbításán, ha

D'

a háromszögön kívül van).
A három kör együtt tehát mindig teljesen lefedi a háromszöget. A háromszög belsejében fekvő minden,

D'

-től különböző,

P

pont tehát legalább egy körön belül van, és ugyanakkor legalább egy körön kívül van, de akkor ugyanez áll a

P

pontra és a körökhöz tartozó gömbökre is. Ezzel tételünket bebizonyítottuk.

Csiszár Imre (Bp., I., Petőfi g. IV. o. t.)