Kezdőlap


Feladat:	716. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Stahl János
Füzet:	1956/május, 145 - 146. oldal		PDF \| MathML
Témakör(ök):	Körök, Síkgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1955/november: 716. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a $B C$ , $C A$ és $A B$ oldalakon keletkező metszéspontokat rendre $X$ , $Y$ , $Z$ -vel (lásd az ábrát).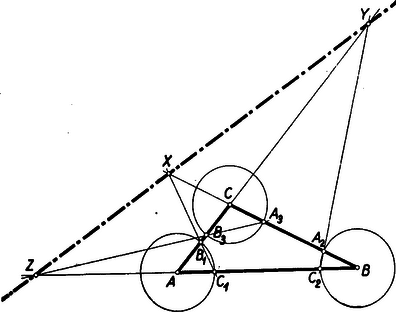

Feltéve, hogy az

A B C

egyenessé el nem fajuló háromszögnek minden oldala különböző hosszúságú, az

X

Y

és

Z

pontok mindig léteznek. Az

A B C

háromszög

B_{1} C_{1}

A_{2} C_{2}

és

A_{3} B_{3}

szelőire rendre felírva a Menelaos-féle tételt:

\begin{matrix} (B C X) (C A B_{1}) (A B C_{1}) = - 1, \\ (C A Y) (A B C_{2}) (B C A_{2}) = - 1, \\ (A B Z) (B C A_{3}) (C A B_{3}) = - 1. \end{matrix}

Mindhárom egyenlőségben a baloldal második és harmadik osztóviszonya az ábrából leolvashatóan kifejezhető a körök közös

r

sugarával és a háromszög

a

b

c

oldalával:

\begin{matrix} (B C X) \frac{b - r}{r} \cdot \frac{r}{c - r} = - 1, \\ (C A Y) \frac{c - r}{r} \cdot \frac{r}{a - r} = - 1, \\ (A B Z) \frac{a - r}{r} \cdot \frac{r}{b - r} = - 1. \end{matrix}

E három egyenlőség szorzata

\begin{matrix} (B C X) (C A Y) (A B Z) = - 1. \end{matrix}

A Menelaos-tétel megfordítása alapján ez éppen azt jelenti, hogy az

X

Y

Z

pontok egy egyenesen vannak.

Stahl János (Bp., VI., Kölcsey g. III. o. t.)

Megjegyzések: 1) Könnyű belátni, hogy tételünk akkor is igaz, ha a köröknek a háromszög oldala meghosszabbításaival való metszéspontjain át húzzuk a szelőket, vagy ha nem kötjük ki, hogy a három kör egymást kizárja.
2) A 3 szelő mindegyike rendre merőleges 1‐1 belső szögfelezőre. Ha

r

minden határon túl közeledik a

0

-hoz (vagyis a körök ponttá zsugorodnak), akkor a szelők (a belső szögfelezőkre merőleges) külső szögfelezőkké válnak. Bizonyított tételünk tehát a külső szögfelezőkre vonatkozó megfelelő (és egyszerűen bizonyítható) tételnek általánosítása.