Kezdőlap


Feladat:	715. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bartha Gyöngyi , Rázga Tamás
Füzet:	1956/május, 143 - 145. oldal		PDF \| MathML
Témakör(ök):	Körök, Középponti és kerületi szögek, Thalesz-kör, Látókörív, Ceva-tétel, Menelaosz-tétel, Szögfelező egyenes, Inverzió, Feladat
Hivatkozás(ok):	Feladatok: 1955/november: 715. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen $P$ a $\hat{B C}$ íven. A $P D$ egyenes az $A B P$ háromszög $P$ csúcsához tartozó belső szögfelezője, mert a félkörívhez tartozó (tehát derékszögű) $A P B$ kerületi szöget két, egyenként egy-egy negyedkörívhez tartozó (tehát $45^{\circ} - 45^{\circ}$ -os) szögre bontja (1. ábra).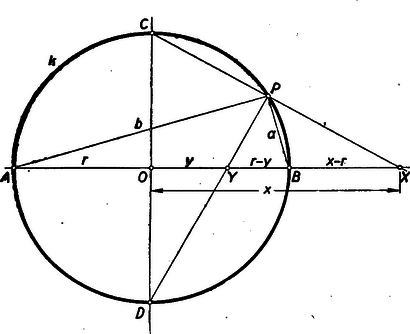

1. ábra

Mivel

P D

felezi az

A P B

szöget és Thales tétele értelmében

P D ⊥ P C

, így

P C

felezi az

A P B ∢

mellékszögét, azaz

P C

A B P

háromszög külső szögfelezője.
Mivel a háromszög bármelyik szögpontjához tartozó belső és külső szögfelező olyan pontokban metszi a szemközti oldalt, amelyeknek az osztóviszonya egyenlő nagyságú, de ellenkező előjelű (Kárteszi: A Menelaos- és Ceva-féle tétel, K. M. L. XI. köt., 3‐4. sz. 67. old.), azért

\begin{matrix} (A B Y) : (A B X) = \frac{b}{a} : (- \frac{b}{a}) = - 1. \end{matrix}

Így az

A

B

;

X

Y

pontok valóban harmonikus pontnégyest alkotnak.
A pontok mozgásának jellemzése:
Fusson

P

\hat{B C}

íven

C

felé. Ekkor

X

A B

-nek

B

-n túli meghosszabbításán fut

B

-től távolodva,

Y

pedig

B O

-n a kör középpontja felé halad.
Ha

P \equiv C

, akkor

Y

O

-ban van, és a

P C

egyenes párhuzamos

A B

-vel, az

X

metszéspont nem is lép fel,

(A B X)

-nek nincs értelme.
Ha

P

továbbhalad a

\hat{C A}

íven, akkor az előbbi ábrának a

C D

átmérőre vonatkozó tükörképét kapjuk. Tükrözéskor az osztóviszony és így a pontnégyes harmonikus volta is változatlanul megmarad.

X

A B

-nek

A

-n túli meghosszabbításán közeledik

A

felé,

Y

O A

szakaszon közeledik ugyancsak

A

felé.
Ha

P \equiv A

, akkor

X \equiv A

és

Y \equiv A

.
Ha

P

\hat{A D}

íven

D

felé halad, akkor az első ábrának az

O

pontra vonatkozó tükörképét kapjuk.

X

A

-tól befelé távolodva

O

felé,

Y

pedig

A

-tól kifelé távolodva mozog.
Ha

P \equiv D

, a

P D

egyenes párhuzamos

A B

-vel,

X

O

-ban van, és most az

Y

metszéspont nem lép fel, vagyis

(A B Y)

-nak nincs értelme.
Ha

P

\hat{D B}

íven mozog, akkor az 1. ábra

A B

-re vonatkozó tükörképét kapjuk.

X

O

-ból

B

felé,

Y

kívülről ugyancsak

B

felé halad.
Ha

P

B

-be érkezik,

B

X

és

Y

ismét egybeesnek.
Megfigyelhetjük, hogy míg a

P

pont befutja a teljes kört, addig

X

is,

Y

is mindig egy-egy irányban haladva egyszer végigfut az

A B

egyenesen.

X

és

Y

egymáshoz képest mindig ellenkező irányban mozog, és

A

, ill.

B

-ben találkoznak. Ha valamelyikük

O

-ban van, akkor a másik nem lép fel (a ,,végtelen''-ben van).

Megjegyzés: Ha a

k

kör sugarát

r

-rel és az

X

és

Y

pontoknak

O

-tól mért távolságát

x

és

y

-nal jelöljük, akkor a

- (A B X) = (A B Y)

így írható:

\begin{matrix} \frac{r + x}{x - r} = \frac{r + y}{r - y} \end{matrix}

amiből

\begin{matrix} x y = r^{2}, vagyis \frac{x}{r} = \frac{r}{y} . \end{matrix}

Ilyenkor azt szoktuk mondani, hogy

X

Y

pontnak (illetőleg fordítva:

Y

X

pontnak) inverze a

k

körre vonatkozólag.

Bartha Gyöngyi (Bp., VIII., Apáczai Csere lg. III. o. t.)

II. megoldás: Messe a

P B

egyenes az

A C

egyenest a

Z

pontban (2. ábra).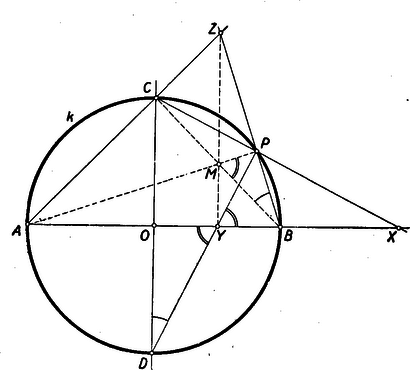

2. ábra

A B Z

háromszögben

A P

és

B C

magasságvonalak. Így

M

a háromszög magasságpontja.

B P M

és

D O Y

háromszögek hasonlóak, mert derékszögűek, és

C B P ∢ = C D P ∢

mint a

\hat{P C}

ívhez tartozó kerületi szögek. Ezért

P M B ∢ =

= O Y D ∢ = P Y B ∢

, vagyis

B P M Y

húrnégyszög. De akkor

M Y ⊥ A B

, és mivel

M

a magasságpont, ezért a

Z M

és

Y M

egyenesek egybeesnek, tehát

Z Y

A B Z Δ

harmadik magasságvonala.
Az

A B Z

háromszögre és az

M

pontra alkalmazva Ceva tételét:

\begin{matrix} (A B Y) (B Z P) (Z A C) = 1, \end{matrix}

(1)

A B Z

háromszögre és az

X P C

egyenesre alkalmazva Menelaos tételét:

\begin{matrix} (A B X) (B Z P) (Z A C) = - 1. \end{matrix}

(2)

(2) és (1) hányadosa:

\begin{matrix} \frac{(A B X)}{(A B Y)} = - 1. \end{matrix}

Rázga Tamás (Bp., II., Rákóczi g. IV. o. t.)