|
| Feladat: |
691. matematika feladat |
Korcsoport: 18- |
Nehézségi fok: nehéz |
| Megoldó(k): |
Almási L. , Bártfai P. , Biczó G. , Bognár P. , Csák J. , Csiszár Imre , Frivaldszky J. , Harza T. , Jakubovics J. , Krem A. , Legéndy K. , Makkai M. , Mecseki A. , Pasitka B. , Quittner P. , Rázga T. , Stahl J. , Szabados J. , Szeidl Béla , Szentai E. , Vásárhelyi B. , Vigassy György , Zsombok Z. |
| Füzet: |
1956/február,
46 - 49. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Mértani helyek, Hiperbola, mint mértani hely, Pont körüli forgatás, Húrnégyszögek, Középponti és kerületi szögek, Feladat |
| Hivatkozás(ok): | Feladatok: 1955/május: 691. matematika feladat |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Jelöljük rendszer tengelyeit -val és -vel. Válasszuk koordináta‐rendszerünk tengelyeit úgy, hogy origója essék egybe a rendszer tengelyeinek metszéspontjával, és a rendszer tengelyeit metsző egyenes legyen merőleges az abszcissza‐tengelyre, az origótól távolságban. Ebben a koordináta‐rendszerben a rendszer tengelyeinek egyenlete és ; a tengelyeket metsző egyenes egyenlete .
Az egyenes metszéspontja az , ill. egyenessel:
Az -hez adjungált pontot úgy nyerjük, hogy megszerkesztjük az -ban -ra emelt merőleges és -ben -re emelt merőleges metszéspontját (1. ábra). 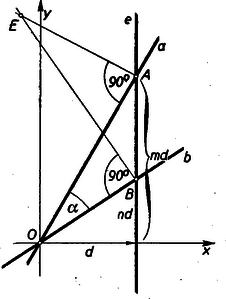 1. ábra
E merőlegesek egyenlete
A forgatás során nem változik. E szög tangense az és iránytényezőkkel ‐ mint ismeretes ‐ a következőképpen fejezhető ki (1), (2) és (3) a forgatással keletkező minden pontra nézve fennáll, tehát ez az egyenletrendszer a keresett mértani hely paraméteres egyenletrendszere. Elvben (1)-ből kifejezhetnénk az paramétert, (2)-ből az -et és a két értéket (3)-ba helyettesítve, mindkettőt kiküszöböltük. Azonban így -re és -re másodfokú egyenlet adódik. Könnyebben célhoz jutunk, ha alkalmas átalakításokkal arra törekszünk, hogy az és értékeket , és -vel kifejezzük.
Ha (1)-ből kivonjuk (2)-t, ismert átalakításokkal összefüggésre jutunk. Ha pedig (1)-et osztjuk -nel, (2)-t -mel és ezután vonjuk le (2)-t (1)-ből, átalakítások után nyerjük (4) és (5)-öt közvetlenül felhasználhatjuk, ha (3)-at ‐ a nevezővel való átszorzás és négyzetreemelés után ‐ így alakítjuk át: | |
(4)-et és (5)-öt behelyettesítve és -tel szorozva Ez az egyenlet hiperbola egyenlete; könnyen hozható a hiperbola egyenletének ismert alakjára. Az | | (6) |
alakból, ahol még leolvasható, hogy a hiperbola középpontja a pozitív tengelyen, az origotól távolságra van; valós tengelyének, amely az tengelyre esik, fél hossza , fél képzetes tengelye pedig . Ezekből a lineáris excentricitásra a középpont abszcisszájával egyenlő érték adódik, tehát a hiperbola egyik fókusza az origó.
| Szeidl Béla (Bp. VIII., Apáczai Csere g. III. o. t.) |
II. megoldás. Jelölés az I. megoldás szerint. Az -ra és -re , ill. pontban emelt merőlegesek annak a parabolának érintői, melynek fókusza az pont, csúcsérintője az egyenes. Eszerint az pontokból az említett parabola , ill. () szög alatt látszik.
A 617. feladat (K. M. L. X. kötet, 1. szám) megoldásával bebizonyítottuk, hogy azon pontok mértani helye, melyekből egy parabola -os, -os szög alatt látszik, hiperbola. Az ott közölt II. megoldással (1955. januári szám, 25. old.) azonos utat követve, de -os szög helyett általános szöggel számolva, a mértani hely egyenleteként a egyenletre jutunk, feltéve, hogy a parabola egyenlete . Jelen esetben azonban a parabola egyenlete és így , . Ha ezen értékeket helyettesítjük (7)-be, akkor megkapjuk a (6) egyenletet.
| Csiszár Imre (Bp. I., Petőfi g. III. o. t.) |
III. megoldás. Az I. megoldás jelöléseit használva a szerkesztés alapján húrnégyszög, a körülírt kör átmérője (miután -ból és -ből derékszög alatt látszik); a körülírt kör középpontja felező pontja: . Rajzoljuk meg az -hoz tartozó középponti szöget és az magasságvonalát, mely az egyenest az húr felezőpontjában, -ben metszi (2. ábra). 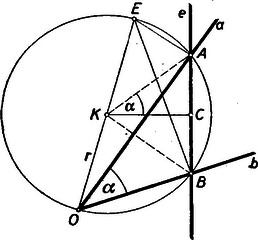 2. ábra
Ha , akkor a távolság 0-vá válik. Tehát a pontok mértani helye maga az egyenes, és így ebben az esetben az pontok mértani helye az -vel párhuzamos, -tól kétszeres távolságban fekvő egyenes. (Ez egyébként kiolvasható az analitikus I. megoldásból is.)
| Vigassy György (Bp. I., Petőfi g. IV. o. t.) |
|
|
 PDF |
PDF |  MathML
MathML 
