Kezdőlap


Feladat:	SCMF0675	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bártfai Pál , Kirz János , Ványai László
Füzet:	1955/december, 138 - 140. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Feladat
Hivatkozás(ok):	Feladatok: SCMF0675 feladat dekódolása nem sikerült. 1955/március: SCMF0675

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Válasszuk $Σ (90^{\circ})$ rendszerünk tengelyeit egy derékszögű koordinátarendszer tengelyeiül. Az $r$ sugarú kör középpontja az origo, tehát egyenlete $x^{2} + y^{2} = r^{2}$ .
Legyenek az érintő egyenes $P$ érintési pontjának koordinátái $x_{1}, y_{1}$ . Az érintő egyenlete ekkor $x_{1} x + y_{1} y = r^{2}$ .
Ennek az egyenesnek a tengelyekkel való metszéspontjai adják az $S$ pont koordinátáit:

\begin{matrix} x = \frac{r^{2}}{x_{1}}, y = \frac{r^{2}}{x_{2}} . \end{matrix}

Ebből az érintési pont koordinátái:

x_{1} = \frac{r^{2}}{x}, y_{1} = \frac{r^{2}}{y}

.
Mivel

(x_{1}, y_{1})

a körön van, azért fennáll az

\begin{matrix} {(\frac{r^{2}}{x})}^{2} + {(\frac{r^{2}}{y})}^{2} = r^{2} \end{matrix}

egyenlet.

r^{4}

-nel osztva, nyerjük, hogy az

S

pontok az

\begin{matrix} \frac{1}{x^{2}} + \frac{1}{y^{2}} = \frac{1}{r^{2}} \end{matrix}

görbén helyezkednek el.
Kérdés még, vajon fordítva, a kapott síkgörbe minden pontjához tartozó adjungált egyenes érintője-e a körnek ? A válasz: igen.
Ugyanis a görbe egy tetszőleges

S_{0} (x_{0}, y_{0})

pontjának adjungált egyenese, az

x

és

y

tengelyekből

x_{0}

, illetve

y_{0}

részeket metsz le, és így egyenlete

\begin{matrix} \frac{x}{x_{0}} + \frac{y}{y_{0}} = 1. \end{matrix}

r^{2}

-tel szorozva, nyerjük az adjungált egyenesre

\begin{matrix} \frac{r^{2}}{x_{0}} x + \frac{r^{2}}{y_{0}} y = r^{2}, \end{matrix}

de ez éppen az

r

sugarú kört az

(\frac{r^{2}}{x_{0}}, \frac{r^{2}}{y_{0}})

pontban érintő egyenes egyenlete, minthogy ‐ a feltétel szerint ‐

(x_{0}, y_{0})

kielégíti az

\frac{1}{x^{2}} + \frac{1}{y^{2}} = \frac{1}{γ^{2}}

egyenletet.
A mértani helyként kapott négy egybevágó ágból álló negyedfokú síkgörbe szimmetrikus az origóra (centrálszimmetria), a

- r < x < r

és

- r < y < r

síksávokon belül nincs pontja és az

\begin{matrix} x = \pm r, y = \pm r \end{matrix}

egyenesek az aszimptotái (lásd az ábrát).

Kirz János (Bp. VIII., Apáczai Csere g. IV. o. t.)

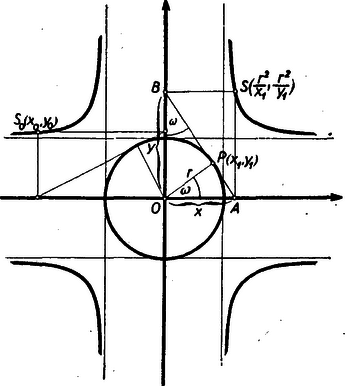II. megoldás: Egy tetszőleges

S (x, y)

pont adjungált egyenese messe a koordinátarendszer tengelyeit az

A

és

B

pontokban.

O A = x

O B = y

. Az

A O B

derékszögű háromszög kétszeres területe (lásd az ábrát) egyrészt

A B \cdot P O =

= r \sqrt[]{x^{2} + y^{2}}

, másrészt

O A \cdot O B = x y

.
Tehát

\begin{matrix} r \sqrt[]{x^{2} + y^{2}} = x y \end{matrix}

a keresett görbe egyenlete.
Négyzetre emelve és

r^{2} x^{2} y^{2}

-tel osztva (az

x = 0

és

y = 0

értékeket kizárva) nyerjük a már ismert

\begin{matrix} \frac{1}{x^{2}} + \frac{1}{y^{2}} = \frac{1}{γ^{2}} \end{matrix}

alakot.

Bártfai Pál (Bp. I. Petőfi g. IV. o. t.)

III. megoldás: Ábránkban az

A O P ∢

-et

ω

-val jelölve, mint merőleges szárú szög az

O B P ∢

is egyenlő

ω

-val.
Az

A P O

és

B P O

derékszögű háromszögekből

\begin{matrix} \frac{r}{x} = cos ω, & (1) \\ \frac{r}{y} = sin ω . & (2) \end{matrix}

(1) és (2) négyzetét összeadva

\begin{matrix} \frac{r^{2}}{x^{2}} + \frac{r^{2}}{y^{2}} = cos^{2} ω + sin^{2} ω = 1, \end{matrix}

vagyis

\begin{matrix} \frac{1}{x^{2}} + \frac{1}{y^{2}} = \frac{1}{r^{2}} . \end{matrix}

Ványai László (Sátoraljaújhely, Kossuth g. III. o. t.)