Kezdőlap


Feladat:	673. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Harza Tibor
Füzet:	1955/november, 106 - 107. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1955/március: 673. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Képzeljük a feladatot megoldottnak. A $C \equiv M \equiv A \equiv B$ triviális megoldáson kívül (midőn is $C A = C B = 0$ ), feladatunknak még három megoldása van, mint azt az ábránk mutatja. A 3 megoldás bármelyikének megszerkesztéséről kimutatható, hogy az egyenértékű egy általános szög harmadolásával. Utóbbi azonban ‐ mint ismeretes ‐ euklidesi értelemben (körzővel és vonalzóval) nem végezhető el, tehát a kívánt $e$ egyenes sem szerkeszthető.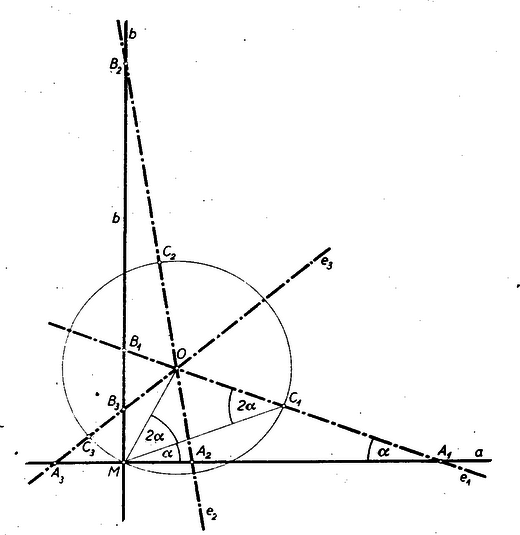

Tekintsük pl. az

e_{1}

egyenest. A betűzést ábránk mutatja. A feltétel szerint

A_{1} C_{1} = C_{1} B_{1}

, és így Thales tétele szerint

M C_{1} = A_{1} C_{1} = C_{1} B_{1}

. Tehát az

A_{1} C_{1} M ▵

egyenlő szárú, és így az alap mellett fekvő szögek egyenlők. Az ábrán ezeket

α

-val jelöltük.
Az

M O C_{1}

egyenlő szárú háromszögben az alap mellett fekvő

M C_{1} O ∢

, mint külső szög, egyenlő

2 α

-val, és így egyszersmind

\begin{matrix} C_{1} M O ∢ = 2 α \end{matrix}

tehát az

M C_{1}

egyenes harmadolja az

A_{1} M O

tetszőlegesen felvett szöget.

Harza Tibor (Székesfehérvár, József Attila g. III. o. t.)