Feladat: 672. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bártfai Pál ,  Csiszár I. ,  Gutai L. ,  Makkai M. ,  Vértes P. ,  Zsombok Z. 
Füzet: 1955/november, 105 - 106. oldal  PDF  |  MathML 
Témakör(ök): Simson-egyenes, Feuerbach-kör, Feladat
Hivatkozás(ok):Feladatok: 1955/március: 672. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a magasságpont M, a körülírt kör középpontja K, a Feuerbach-féle kör középpontja F, a körülírt kör változó átmérőjének végpontjai legyenek P1 és P2, MP1 és MP2 felezőpontjai Q1, ill. Q2, a P1 és P2 pontokhoz tartozó Simson egyenesek s1, és s2 (lásd az ábrát).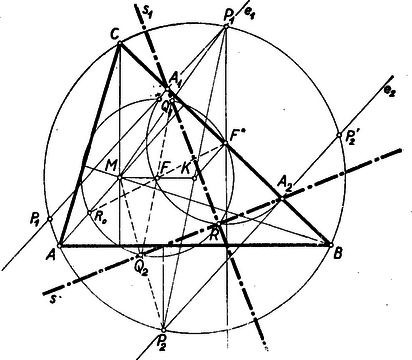

 
 

Abból az ismeretes tételből, hogy M-nek bármely háromszög oldalra vonatkozó tükörképe a körülírt körön van, következik, hogy a körülírt körnek 1:2 arányú kicsinyítése az M-ből, mint hasonlósági centrumból, olyan kör, amely átmegy a magasságvonalak talppontjain, vagyis ez a kicsinyített kör a talpponti háromszög köré írt ún. Feuerbach-féle kör.

(1) E tényből következik, hogy Q1 és Q2 rajta vannak a Feuerbach-féle körön, és e körnek átellenes pontjai.

(2) Másrészt a 659. feladatban bizonyítottuk, Q1 és Q2 rajta van az s1 ill. s2 Simson-egyenesen.
A 667. feladatban kimutattuk azt is, hogy s1 és s2 szöge egyenlő a P1P2⌢ ívhez tartozó kerületi szöggel. Ez utóbbi jelen esetben 90∘, tehát s1⊥s2, vagyis s1, és s2 R metszéspontja a Thales-tétel értelmében és (2) szerint a Q1Q2, mint átmérő, fölé írt körön, vagyis (1) szerint a Feuerbach-féle körön van.
A mértani hely fogalma annak kimutatását is követeli, hogy fordítva a Feuerbach-féle kör minden pontján át találhatók olyan s1 és s2 Simson-egyenesek, amelyekhez tartozó P1 és P2 pontok a körülírt kör átellenes pontjai.
E megfordítás igazolásához előbb állapítsuk meg a következőket, Ha F*-gal jelöljük a BC oldal felezőpontját (amelyen egyébként a Feuerbach-féle kör szintén átmegy, és F*K⊥BC), akkor P1P2 átmérő lévén, e pontok A1A2 vetületei a BC oldalon éppen a Simson-egyenes értelmezésénél fogva az s1, ill. s2-nek pontjai, másrészt F*A1=F*A2. Mivel s1⊥s2 azért Thales-tétele értelmében az F* körül, mint középpont körül F*A1-F*A2 sugárral rajzolt kör átmegy az R ponton.
Ennek alapján a Feuerbach-féle kör egy tetszőleges R pontjához a körülírt körön keresett átellenes pontpár így szerkeszthető meg: a BC oldal F* felezőpontja, mint középpont körül R-en átmenő kört húzunk. Ez messe a BC oldalt A1 és A2 pontban. Az A1 és A2-ben BC-re állított e1 és e2 merőlegesek egymás tükörképei a K középpontra, mert F*K az A1A2 szakasznak is felező merőlegese. Ennek folytán az e1 és e2 egyeneseknek a BC egyenes ellenkező oldalára eső P1,P2, és P'1,P'2, metszéspont párjai a háromszög köré írt körrel ‐ ha metszik ez egyenesek a kört ‐ átellenes pontpárokat adnak. A hozzájuk tartozó két-két Simson-egyenes átmegy A1-en, ill. A2-n, merőleges egymásra, tehát metszéspontjuk az F* körül rajzolt körön van, ezen kívül, a megoldás első része szerint, rajta van a Feuerbach-féle körön is. Így a két pontpárhoz tartozó Simson-féle egyenes-párok egyike R-ben, másika a két kör másik, R' metszéspontjában metszi egymást. Ki kell még zárni annak lehetőségét, hogy az e1 és e2 egyenesek a körülírt körön kívül haladjanak. Az A1 és A2 pontok akkor vannak legtávolabb egymástól, ha R a Feuerbach-kör F*-gal átellenes R0 pontjába kerül. Ekkor távolsága ‐ és így A1 és A2 távolsága is ‐ F*-tól a Feuerbach-kör átmérőjével, tehát a körülírt kör sugarával egyenlő. Az ennek megfelelő e1 és e2 egyenesek érintik a körülírt kört, minden más esetben e két szélső egyenes közt haladnak, tehát metszik a körülírt kört.
Ezzel a feladat állítását teljes egészében bebizonyítottuk.
 

Bártfai Pál (Bp. I., Petőfi g. IV. o. t.)