Kezdőlap


Feladat:	666. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bakos T. , Bártfai P. , Beke Gy. , Beliczky G. , Benkő B. , Benkő Gy. , Biczó Géza , Csiszár Imre , Daróczy Z. , Darvas I. , Forgó G. és I. , Frank Gy. , Frivaldszky S. , Gutai László , Győrösi P. , Horváth J. , Katona P. , Kim Kvang Jan , Kirz J. , Kiss P. , Krammer G. , Krem A. , Legéndy K. , Lindner I. , Litvai J. , Makkai M. , Mecseki A. , Pátkay Gy. , Perneczky L. , Rázga T. , Schipp F. , Seeler N. , Stáhl J. , Szentai E. , Tarlacz L. , Udvari A. , Vásárhelyi B. , Vértes A. , Zsombok Z.
Füzet:	1955/november, 98 - 100. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték-feladatok differenciálszámítás nélkül, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1955/február: 666. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Feltesszük, hogy $a$ és $b$ nem párhuzamos egyenesek. Toljuk el az $a$ egyenest önmagával párhuzamosan $a'$ helyzetbe, úgy, hogy két megfelelő pont pl. $A_{1}$ és $B_{1}$ egybeessék (1. ábra).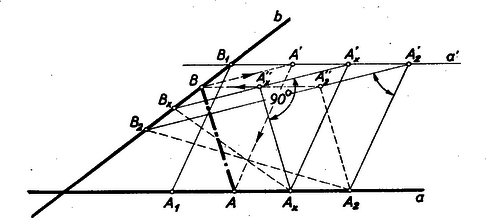

1. ábra

Legyen

A'_{x}

és

B_{x}

a'

, ill.

b

egyenes egy egymásnak megfelelő pontpárja, akkor ‐ mivel a mozgás mindkét egyenesen egyenletes ‐

A'_{x} B_{x}

összekötő egyenes párhuzamos

A'_{2} B_{2}

-vel.
Az

A_{x} A'_{x} B_{x}

változó háromszögekben az

A_{x} A'_{x}

oldal a párhuzamos eltolás folytán egyenlő és párhuzamos

A_{1} B_{1}

-gyel, továbbá az

A_{x} A'_{x} B_{x} ∢

is állandóan megfelelő szöge az

A_{2} A'_{2} B_{2} ∢

-nek. Az

A_{x} B_{x}

oldal akkor minimális, ha

A_{x} B_{x} \equiv A B ⊥ A' B

, vagyis ha

A B

párhuzamos az

A_{x} A'_{x} B_{x ▵}

-ben az

A_{x}

csúcsponthoz tartozó

A_{x} A''_{x}

magassággal.
A szerkesztés menete: a tetszőlegesen felvett

A_{x} A'_{x} B_{x}

háromszögben, tehát pl. az

A_{2} A'_{2} B_{2 ▵}

-ben megszerkesztjük az

A_{2}

-ből kiinduló magasság

A''_{2}

talppontját, ezen át

a

-val húzott párhuzamos egyenes metszi ki a

b

egyenesből a keresett

B

pontot.

B A ∥ A''_{2} A_{2}

Megjegyzés: Ha

a ∥ b

, ‐ és a két pont nem mozog egyenlő sebességgel egy irányban ‐ ez esetben

A B

akkor minimális, ha

A B

merőleges

a

-ra és

b

-re. Belátható, hogy ez esetben a megfelelő pontpárokat összekötő egyenesek egy ponton mennek keresztül. Ennek igazolása nélkül is bizonyíthatjuk a következő szerkesztés helyességét: az

A_{1} B_{1}

és

A_{2} B_{2}

egyenesek

M

metszéspontjából merőlegest bocsátunk

a

-ra, ez metszi ki a minimális

A B

szakaszt.

A

és

B

valóban egymásnak megfelelő pontok, mert

B_{1} B : A_{1} A = M B : M A = B_{1} B_{2} : A_{1} A_{2}

.
Ha a két pont egy irányban mozog egyenlő sebességgel, akkor (az

M

pont nem létezik) és a két pont távolsága állandó marad.

Gutai László (Bp. IV., Könyves Kálmán g. IV. o. t.)

II. megoldás: Jelöljük

a

és

b

metszéspontját

M

-mel. Szerkesszük meg az

A_{1}, B_{1}, M

és

A_{2}, B_{2}, M

pontokon átmenő köröket (2. ábra).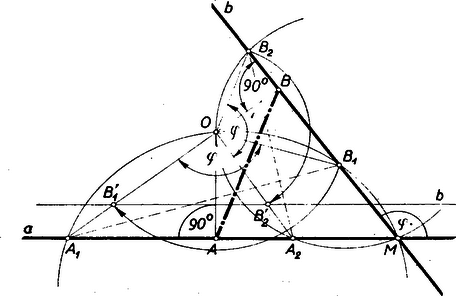

2. ábra

Legyen e két kör metszéspontja

O

. Ha

φ

-vel jelöljük az

a, b

egyenesek által bezárt hegyes- vagy tompaszöget aszerint, hogy

O

tompa- vagy hegyesszögű tartományban van, akkor a kerületi szögek tétele szerint

A_{1} O B_{1} ∢ = φ

és

A_{2} O B_{2} ∢ = φ

. Forgassuk el a

b

egyenest

O

körül

φ

szöggel úgy, hogy a

B_{1}

és

B_{2}

pontok

B'_{1}

és

B'_{2}

elforgatása az

O A_{1}

ill.

O A_{2}

egyenesekre kerüljenek, akkor

B'_{1} B'_{2} = b' ∥ a

. Az elforgatott

B

pontokra alkalmazva

\frac{O A_{1}}{O B'_{1}} = \frac{O A_{1}}{O B_{1}}

arányú nyújtást (vagy zsugorítást), az elforgatott

B

pontsor átmegy az

A

pontsorba. Ennél a forgatva-nyújtásnál az

A_{x} O B_{x}

háromszögek mind hasonlóak, mert

O

-nál a

φ

szög állandó és e szöget bezáró oldalak aránya egyenlő. Tehát

A_{x} B_{x}

akkor minimális, ha

O A_{x}

(és ugyanakkor

O B_{x}

) minimális, vagyis

O A_{x} \equiv O A ⊥ a

, és

O B_{x} \equiv O B ⊥ b

Csiszár Imre (Bp. I., Petőfi g. III. o. t.)

III. megoldás: Gönyei Antal

≫

Egy geometriai rokonságról

≪

c. cikkének (K. M. L. 1955. januári szám) 6. pontjában bebizonyítja, hogy ha két egyenesen hasonló pontsorokat veszünk fel, akkor az egymásnak megfelelő pontokban emelt merőlegesek metszéspontjai egy egyenesen sorakoznak. E tételt felhasználva, megszerkesztjük az

S_{1} S_{2} = s

egyenest (3. ábra).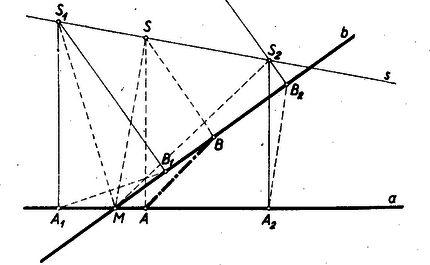

3. ábra

Thales tétele értelmében az

M A_{x} S_{x} B_{x}

ill.

M A_{x} B_{x} S_{x}

négyszögek mind húrnégyszögek, amelyek köré írt kör átmérője

M S_{x}

, és az

A_{x} B_{x}

oldalhoz, mint húrhoz, tartozó kerületi szög pedig az

a

és

b

egyenesek szöge. Különböző átmérőjű körökben egyenlő kerületi szögekhez tartozó húrok közül a legkisebb átmérőjű körben levő húr a legkisebb, tehát

A_{x} B_{x} \equiv A B

minimális, ha

M S_{x} \equiv M S ⊥ s

Biczó Géza (Bp. II., Rákóczi g. IV. o. t.)